CMU15-445 Lab2 Hash Index
Hash Index
声明:此为2021 CMU 15-445 Lab2,实验任务为完成Extendible Hash Table相关设施的编码
Extendible Hashing
(以下统一译为“可扩展哈希”)静态哈希策略因为其桶数量是固定的,因此必须要用到溢出桶(overflow bucket),不能应对数据库文件大小的变化。
可扩展哈希作为动态哈希策略,可以针对数据库文件的大小变化而进行桶(bucket)的分裂和合并,并且开销能够接受,理由下面解释。
基本构成
可扩展哈希维护一个全局深度(global depth,以下简称为gd),并为每一个桶分配局部深度(local depth,以下简称为ld)。
可扩展哈希表当前的桶数量为$2^{gd}$。如果此时存放记录的页(以下简称为页)和每个桶一一对应,这很符合认知。如果页的数量比桶的数量要少,那么必然有多个桶为指向同一个页,同时要让落到这些桶的记录的哈希值相同。
可扩展哈希是通过将记录的哈希值的前缀与桶关联来达成这个目的。这样一来,哈希值是00前缀的都会指向同一个页,并且随着gd的变化也不会变化,也就是说在扩容的时候我们不需要处理它们的再分配(rehash)。因此可扩展哈希的扩容开销主要是集中在要分裂的那个桶上。
不难想到,在整个哈希表,以(1 << 前缀长度)作为步长遍历到的所有桶都会与该桶指向同一个页,
而该前缀长度就是我们需要记录的ld,继而1 << (gd - ld)就是表中指向该页的桶数量。为了方便称呼,这里将这些指向同一页的桶称作同一层次的桶。
到这里,想必读者已经理解了gd和ld的作用了:
- gd:记录当前哈希表的桶数量,扩容和缩容的判据之一
- ld:记录到同一层次的桶的步长,与gd结合可以得出有多少桶指向该页,也是扩容和缩容的判据之一
相对传统的分离链表法(separate list),可扩展哈希更适合数据库:
- 可扩展哈希的桶的大小就是一个
page(4K/16k/64k),具有良好的空间局部性(spatial locality),相比分离链表法往往采用的是链表,空间局部性差 - 退一步说,分离链表法也可以选一个桶作为list。但是分离链表法采用的是很平凡的槽数组(slots),一般分配桶的策略就是
hash(record) % size(slots),当扩容时,可能会出现大量的桶的引用移动槽位,而可扩展的扩容是稳定的,扩容的另一半定位桶的引用为原来的桶的页以及一个对新页的重定位。
可扩展哈希的缺点也很明显:
- 编码难度大(通过该实验深刻体会到)
- 扩展的速率太快,呈2的幂增长,即指数增长,因此扩容和缩容的开销在表比较大的时候会很高(改善方法:
线性哈希(linear hashing))
Insert
Introduction
初始时,gd = ld = 0,即只有一个桶和一个页: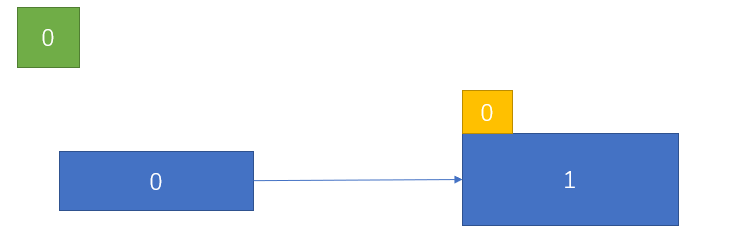
所以所有记录必然会落到该桶里,全部指向同一个页,所以必然需要扩容和分裂。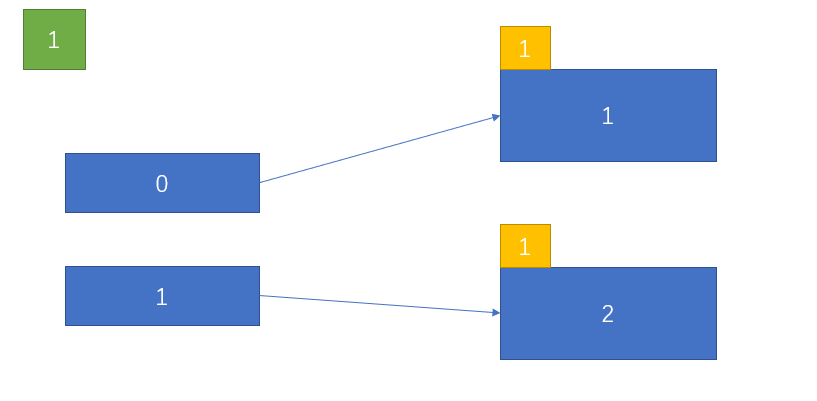
其中任意一页满时,也需要扩容(这里假设页2已满):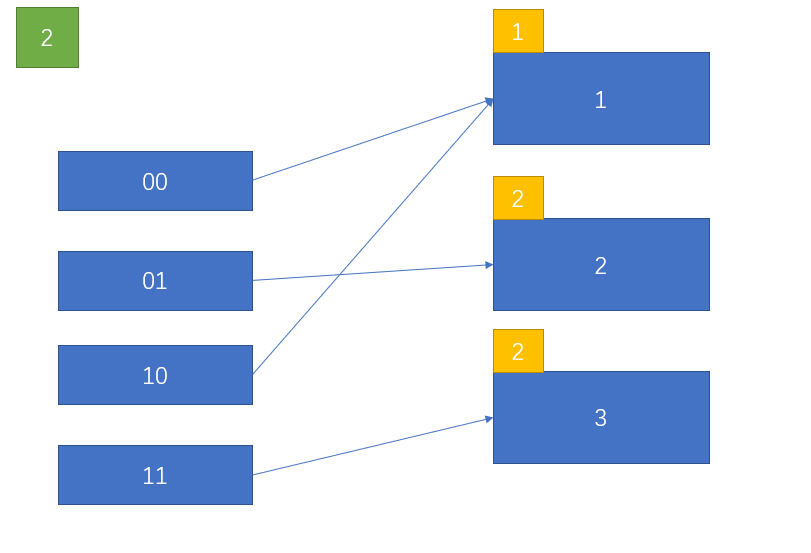
原本指向页2的桶是01,这里由于分离为两个页:2和3,可是表的大小是2,因此必须扩容才有新的桶指向这个新页。那么决定哪个桶指向新页呢?这里涉及到split image index(以下称为分裂映象索引)的计算。
分裂映像索引就是原来分裂的桶在新哈希表中的镜像对称位置的桶的索引。不难看出,除了最高位以外,低位均相同。低位总共占的位数为gd - 1,同时也等于ld-1,这是必然的,因为此时只有一个引用指向各自的页,即gd=ld。
我们再来考虑一个例子就知道那个公式是对的了: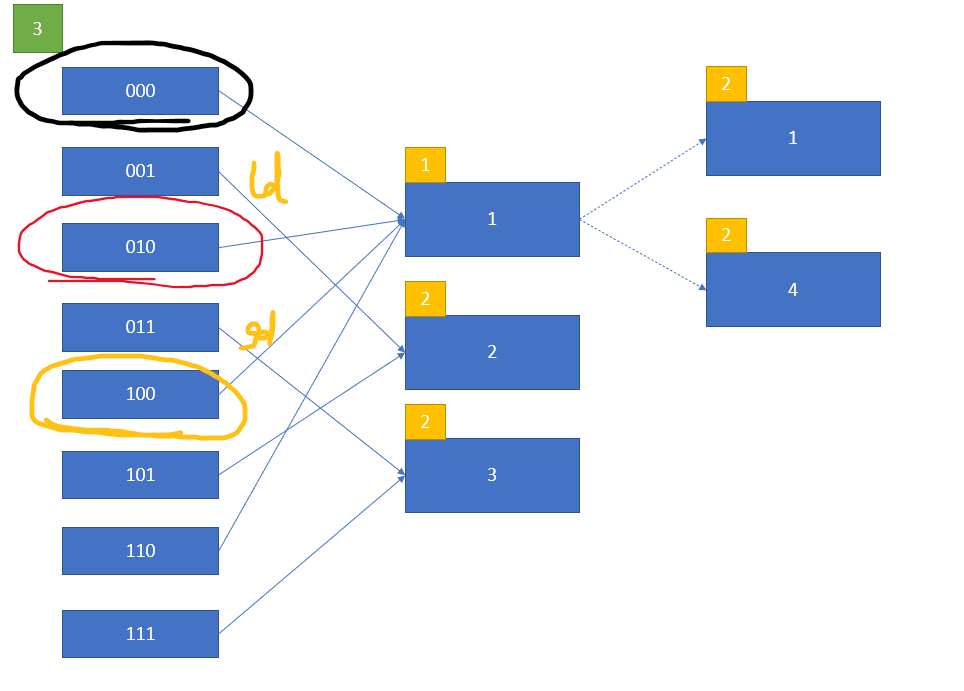
如果是通过gd得到的分裂映像索引,实际上它可能会是新的同一层次的桶,它们的前缀仍然会相同,所以会共享同一个页。
而通过ld得到的分裂映像索引不会如此,因为它的掩码必然会使新的前缀的最高位取反,其他位不变,即绝对不会与它在同一个层次,比如这里的基于ld得到的掩码就是010,与000异或得到010。
这个掩码的获取利用了异或的特性:0 ^ n = n,1 ^ n = ~n
所以SplitImageIndex的伪码如下:1
2
3
4
5
6uint32_t SplitImageIndex(uint32_t bucket_idx) noexcept
{
// ld is the new local depth, so minus 1 first
// \note 1 << (negative) is UB(undefined behavior)
return bucket_idx ^ (1 << ((ld == 0 ? 0 : ld - 1)));
}
接着上一张图讲解。如果ld < gd,那么如何处理呢?它没有必要扩容对吧,因为有多余的引用可以转移过来,原来前缀是0的记录现在可以平分到00和10中去,而这些前缀都有(因为当前最长前缀=gd)。
因为分裂映像索引与该位置在新的ld下不会在同一层次,并且步长翻倍,因此可以很自然地将各自的引用平分即可。
Algorithm
插入:
- 得到对应的桶索引,桶指向的页号,gd,ld等
- 尝试插入,一般情况,插入都会成功,如失败,返回false
- 插入之后,如果页满,那么进行分裂操作
- 返回是否成功
分裂操作:
- 请求BufferPool分配新页,分配失败,直接返回false
- ld(bucket) = ld(bucket) + 1
- 得到桶对应的分裂映像索引,并将其 ld 设为 ld(bucket)
- 根据gd和ld的比较,决定是否需要扩容
3.1 需要扩容
3.1.1 gd = gd + 1
3.1.1 分裂映像索引的桶指向新页,除此之外的另一半的其他桶指向和原来一半的桶相同的页
3.2 不需要扩容
3.2.1 分裂映像索引指向新页,并以新的步长上下两个方向更新同一个层次的桶的指向
3.2.1 同样,以新的步长沿上下方向更新同一个层次的桶的ld
Remove
既然插入涉及哈希表的扩容(expand/grow),那么删除必然涉及哈希表的缩容(shrink)。
但是在考虑缩容之前我们来想想,如果一个页已空,那么它涉及到桶的指向变更。
之前分裂过的两个桶分别指向了不同的页,那么我们可以考虑将桶重定向为分裂映像指向的页,并使其ld减1。这个操作称为归并(merge)。但是有个问题,那个桶可能又分离过一次,所以一个前提条件是ld(bucket) = ld(split_image)。
其他的前提条件有
gd != 0,此时只有一个页ld(bucket) != 0,所有桶都指向同一个页,即使ld(bucket) = ld(split_image)也没有必要归并了,因为ld没有减小的必要
接下来,我们来讨论shrink操作。
首先什么时候可以shrink呢?页的数量不大于桶的一半,即每个页至少有两个桶指向它。那么这时候另一半就很多余,因为即便此时的gd = gd - 1,它们得到的前缀也会落到正确的桶内(比如00和10指向同一个页,即使前缀变成0也依然正确)
所以shrink操作伪码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18bool CanShrink() noexcept
{
for (auto ld : bucket_local_depths_) {
assert(ld <= gd);
if (ld == gd) {
return false;
}
}
return true;
}
void Shrink() noexcept
{
if (Canshrink()) {
--gd_;
}
}
merge的大部分过程可以看作是插入的逆过程:
如果满足上述三个条件,那么对该桶的当前同一层次的桶都更新指向和ld,同时更新与分裂映像在同一层次的桶的ld。
但是有个问题如果这个页接着也空了,会如何呢?
拿这个举例子吧,00和10已经归并过一次了,因此它们通过此时的ld得到的分裂映像索引会是01或11,而它们的ld是2,因此无法归并。我们什么都不能做,因为01和11的前缀还得落到这两个桶中从而得知它们确实指向一个空页。
因此,这里我们还需要提供一个操作去归并这样的空页,不然最后即使整个表都是空页,然而gd != 0。
这里我是采用桶指向的页是否为空,利用了目录页(directory)的空余内容维护了512字节的映射表来合并空页。因为如果我采用检查页是否为空,那么就必须对每个页调用FetchPage(),这就很糟糕了。因此往往扩展哈希是不鼓励提供shrink操作的,很多文章不会涉及该操作。
如果这个表都是空页,那么就是缩容一半,直到不能再缩为止。





