STL RBTree设计
rbtree的总体设计
STL的rbtree为了可以快速索取到有序序列的最小值和最大值,用到了header,它的left指向最小元素,right指向最大元素,而根节点也是通过它来获取:建立parent链接,更进一步地了识别这种特殊节点,建立特殊的关系:互为parent,整个树只有这两个节点有这样的特性,为了区别root和header,设置header颜色为红。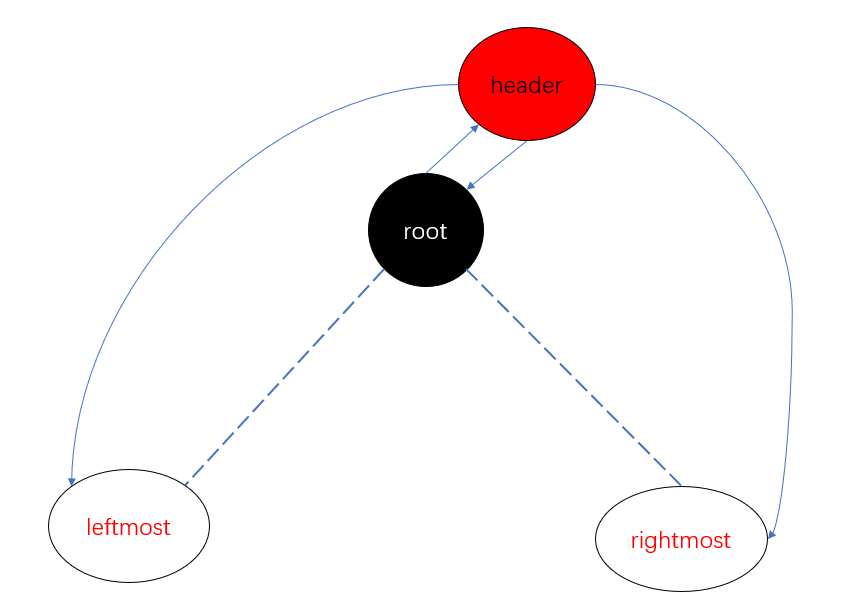
除此之外,header还维护总结点数,即size,为了可以O(1)获取。
header在逻辑上是value无法访问的节点,因此适合做end(),在逻辑上它是“最大值”,最大元素通过operator++应该得到header。1
2
3
4struct RBTreeHeader {
RBTreeBaseNode header; // see next section
std::size_t node_count;
};
起初,没有节点的时候,header需要设置初始状态,我们令left和right都指向自身(这个对于insert处理有用),而parent设置为NULL
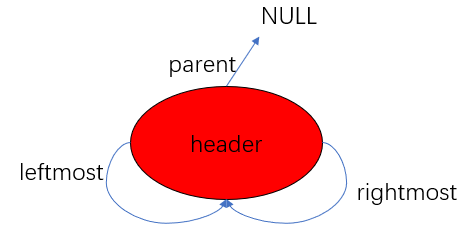
rbtree节点的设计
为了使得所有模板实例都可以共享相同的算法(可以减小生成可执行文件大小),设计了两种节点,它们的区别仅在于value字段有无,即仅拥有链接属性和颜色。这样我们可以在源文件(.cc)写对应的算法实现,头文件仅保留其声明。1
2
3
4
5
6
7
8
9
10
11
12
13
14struct RBTreeBaseNode {
RBTreeColor color;
BasePtr parent;
BasePtr left;
BasePtr right;
//...
};
template<typename Val>
struct RBTreeNode : /* public */ RBTreeBaseNode{
// ... some helper
Val val;
};
rbtree迭代器的设计
rbtree的迭代器是bidirectional迭代器,其算法基础是BST中出现的前继(predecessor)和后继(successor)的算法,只不过加了header我们需要额外处理一下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52RBTreeBaseNode const*
RBTreeIncrement(RBTreeBaseNode const* node) noexcept {
// if right subtree is not empty
// search the minimum of right subtree
// otherwise, search the least ancestor of given node whose
// left child is also an ancestor
if (node->right != nullptr) {
return RBTreeBaseNode::Minimum(node->right);
} else {
// if right of root is null
// then header.left = header.right = node
// so we should handle it explicitly
auto p = node->parent;
while (p->right == node){
node = p;
p = node->parent;
}
// if node = root, p = header
// now, root is maximum, node = header, p = node
// i.e. return end()
if (node->right == p)
return node;
return p;
}
}
RBTreeBaseNode const*
RBTreeDecrement(RBTreeBaseNode const* node) noexcept {
// if node is header, should return leftmost
// because node->parent->parent = node not only header but also root
// set header.color to red is a implemetation trick
if (node->parent->parent == node
&& node->color == RBTreeColor::Red)
return node->right;
if (node->left != nullptr)
return RBTreeBaseNode::Maximum(node->left);
else {
auto p = node->parent;
while (p->left == node) {
node = p;
p = node->parent;
}
// althrough node = root => p = root
// we don't want return header that make begin() and begin() be a loop
// so trivially return p
return p;
}
}
迭代器中的operator++和operator—就是这两个函数的wrapper。
迭代器本身设计其实比较简单。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// This is just a demo
// code is more complex in fact
template<typename T>
struct RBTreeIterator {
typedef RBTreeBaseNode* RBTreeBasePtr;
typedef RBTreeNode<T>* LinkType;
RBTreeBasePtr node_;
// helper...
};
template<typename T>
struct RBTreeConstIterator {
typedef RBTreeBaseNode const* RBTreeBaseConstPtr;
typedef RBTreeNode<T> const* LinkType;
RBTreeBaseConstPtr* node_;
// should provide a conversion constructor make
// iterator -> const_iterator is possible
// helper...
};
插入的rebalance算法
主要涉及的理论在另一篇博客中已经写过了。
这里主要讲下接口设计。
为了分离的彻底,将新插入节点和parent以及header作为参数,在该函数中进行链接的设置,因为BaseNode没有value字段,所以我们需要一个参数表示是否插入左边。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35/**
* @brief relink inserted node and its parent and fixup to maintain red-black property
* @param insert_left indicate if insert left(i.e. left must be null)
* @param x inserted node
* @param p parents of x
* @param header header sentinel pointing to leftmost, rightmost and root
*/
void RBTreeInsertAndFixup(
const bool insert_left,
RBTreeBaseNode* x,
RBTreeBaseNode* p,
RBTreeBaseNode* header) noexcept {
if(insert_left){
p->left = x;
// if p is header, update root
// and set rightmost and leftmost
if(p == header){
header->parent = x;
header->right = x;
// if p is the leftmost, update it
}else if(p == header->left){
header->left = x;
}
}else{
p->right = x;
// if p is the rightmost, update it
if(p == header->right)
header->right = x;
}
x->parent = p;
RBTreeInsertFixup(x, header->parent);
}
最关键的RBTreeInsertFixup相对那篇博客提到的来说更为复杂,因为这里没有NIL哨兵,因此需要将NULL或nullptr的情形考虑为NIL,即黑色哨兵,其他同那篇博客(删除亦然)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66/**
* @brief Red-Black rebalance alghorithm for insert
* @param z inserted new node
* @param root root of rbtree
* @return void
* @see https://conzxy.github.io/2021/01/26/CLRS/Search-Tree/BlackRedTree/
*/
static void
RBTreeInsertFixup(RBTreeBaseNode* z, RBTreeBaseNode*& root){
while(z->parent->color == RBTreeColor::Red
&& z != root ) {
// z is the left child
if(z->parent->parent->left == z->parent){
auto uncle = z->parent->parent->right;
//CASE1 : uncle's color is red
//recolor uncle and parent, then new_node up by 2 level(grandpa)
if(uncle && uncle->color == RBTreeColor::Red){
z->parent->color = RBTreeColor::Black;
uncle->color = RBTreeColor::Black;
z->parent->parent->color = RBTreeColor::Red;
z = z->parent->parent;
}
// if uncle is NULL, it is also NIL leaf whose color is black
else {
//uncle's color is BLACK
//CASE2: parent right is new_node
//now, grandpa, parent and new_node are not in one line
//so left rotate parent make them in one change to CASE3
if(z->parent->right == z){
z = z->parent;
LeftRotation(root, z);
}
//CASE3: parent left is new_node
//just right rotate the grandpa, and recolor
//that rebalance the RBTree
z->parent->parent->color = RBTreeColor::Red;
z->parent->color = RBTreeColor::Black;
RightRotation(root, z->parent->parent);
}
}
else{
//symmetric cases
auto uncle = z->parent->parent->left;
if(uncle && uncle->color == RBTreeColor::Red){
z->parent->color = RBTreeColor::Black;
uncle->color = RBTreeColor::Black;
z->parent->parent->color = RBTreeColor::Red;
z = z->parent->parent;
}
else{
if(z->parent->left == z){
z = z->parent;
RightRotation(root, z);
}
z->parent->parent->color = RBTreeColor::Red;
z->parent->color = RBTreeColor::Black;
LeftRotation(root, z->parent->parent);
}
}//if(grandpa->left == parent)
}//while
// when case 1 up to root, recolor root to maintain property 2
root->color = RBTreeColor::Black;
}
rbtree的插入接口
这些都是插入的准备工作,因为STL分为mutilset/map和set/map,其区别在于是否允许相同的key元素存在于容器,这个实现主要是通过插入接口实现两组:
- XXXUnique()
- XXXEqual()
并且在c++11由于move semantic和perfect forward的引入,XXXset/map系列也引入了emplaceXXX()接口,其特点在于in place构造元素,而不是用户在外面构造好了在传进来,这样省去了一次移动构造或拷贝构造(移动构造可能成本低,但也不是无成本)
emplace()和insert()的unique版本对于相同key的元素的取舍有所区别:
- insert判断不可以插入时,直接舍弃,不会创造新节点
- emplace需要先创造新节点,判断为不可以插入时,需要销毁该节点
为什么会这样,是因为emplace传入的只是构造该value的参数而已,不是已构造的值,所以无法获取到对应的key去比较,只能先创造再比较。
所以我比较推荐如果不是multiXXX容器,不建议使用emplace,否则插入相同key元素代价比较大
但是如果可以保证不会插入相同key的话,还是推荐emplace的(理由见上)
Unique/Equal设计
根据C++标准,rbtree应该只需要弱序谓词(<)就能功能,因此不会传入判断key是否相同的谓词,因此我们必须用 < 来实现==的判断
我们用一个bool变量cmp表示比较结果
- true — insert into left(if new node is root, also insert to left)
- false — insert into right
如果cmp为true,那么我们得到了key < parent
我们用pre(parent)表示parent的前继,
如果key $\in$ (pre(parent), parent),说明还有个hole可以塞进去
否则说明pre(parent) = key
如果cmp为false,我们得到了key >= parent
如果我们可以得到key > parent,就否决了=,那么亦然可以说明它可以塞进去
我们统一下逻辑:
- cmp = false, key > parent ==> success
- cmp = true, key > pre(parent) ==> success
假如pre(parent)不存在,即是leftmost,那么没有必要进一步比较,它会成为新的leftmost
用一个if就可以表达这个逻辑
在BST的博客中,讲述了如何插入新节点到BST中去:
用trailing pointer去跟踪,直到找到一块空地(hole),此时它表示的即为hole的parent,至于是左是右,可以通过cmp表示(不过那个博客写的是equal版本的)
先说一下,我们通过哪个接口调用RBTreeInsertAndFixup():
因为insert和emplace对于新节点采取的策略是不一样的,采取统一的接口更为方便。
如果是用1
2template<typename... Args>
iterator EmplaceAux(Args&&... args, BasePtr cur, BasePtr p);
因为这个接口就意味着必然要构造新节点,舍弃时必须销毁,我们应该把构造新节点的部分分离出来,
所以用新节点作为参数是最为合适的
如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33template<typename Arg, typename = TinySTL::Enable_if_t<
Is_convertible<Arg, value_type>::value>>
iterator InsertAux(Arg&& arg, BasePtr cur, BasePtr p) {
auto new_node = CreateNode(STL_FORWARD(Arg, arg));
STL_TRY {
EmplaceAux(new_node, cur, p);
} CATCH_ALL {
DropNode(new_node);
RETHROW
}
return new_node;
}
iterator EmplaceAux(LinkType new_node, BasePtr cur, BasePtr p) {
// insert_left used for RBTreeInsertAndFixup() to reset link
//
// If cur is not nullptr, we can think caller insert into left
// !This property can be used for GetInsertXXXPos() to reduce the
// overhead of one compare
//
// if cur is nullptr, and it is not header, we should use key_comp()
// to determine if insert into left or right
assert(new_node);
bool insert_left = cur || p == Header() ||
key_comp()(_Key(new_node), _Key(p));
RBTreeInsertAndFixup(insert_left, new_node, p, Header());
++impl_.node_count;
return new_node;
}
InsertAux由于Arg就是表示值,所以在调用该函数之前就已经决定了是否要插入,可以创造玩节点后再转发给EmplaceAux()
为了适用于emplace和insert,我们用key作为参数写一个接口可以获取cur和parent1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83template<typename K, typename V, typename GK, typename CP, typename Alloc>
auto RBTree<K, V, GK, CP, Alloc>::GetInsertEqualPos(key_type const& key)
-> pair<BasePtr, BasePtr> {
auto y = Header();
auto x = Root();
while(x){
y = x;
x = key_comp()(key, _Key(x)) ? x->left : x->right;
}
return make_pair(x, y);
}
template<typename K, typename V, typename GK, typename CP, typename Alloc>
auto RBTree<K, V, GK, CP, Alloc>::GetInsertUniquePos(key_type const& key)
-> pair<BasePtr, BasePtr> {
// use y as a trailing pointer to track the new_node
auto y = Header();
auto x = Root();
// indicate new_node will insert into left or right
// that is, position of "hole"
bool cmp_res = true;
while(x){
y = x;
cmp_res = key_comp()(key, _Key(x));
x = cmp_res ? x->left : x->right;
}
// if cmp_res is false, is is just a y
// otherwise it is predecessor of y when y is not leftmost node
iterator pre(y);
// if cmp_res is true, <1>
// there two cases:
// 1) left is hole
// we must compare new_node with predecessor of y
// because it in right subtree of seccessor, i.e., less than or equal it.
// But, if y is leftmost node, it is no need to compare and just insert.
//
// 2) y is header
// just insert root to its left and reset leftmost and rightmost
//
// Why that must be a unique key?
// suppose cmp_res is true and not case2,
// then we have a inequality: Predecessor(p) <= val < p.val,
// if not val >= predecessor(p), we can't get val < p.val(proof by contradiction)
// if key_comp(pre.val, val) is false indicates that exists a value = val,
// Therefore, pre.val < val can prove val is unique,
// that is, there is a unique "hole" in the sorted sequence.
typedef TinySTL::pair<BasePtr, BasePtr> Res;
if(cmp_res){ // <1>
// there are two cases:
// 1) y is header(only when tree is empty)
// 2) y is real leftmost
// but can return the same result
// @see comments of EmplaceAux()
if(y == LeftMost())
return Res{ x, y };
else
--pre;
}
assert(!x);
// if cmp_res is false and pre is header(i.e. end())
// we should exclude it, and also insert it, beacuse it have not key field
if(key_comp()(_Key(pre.node_), key)) { //<2>
// @note
// we don't reset root here, just forward RBTreeInsertAndFixup()
// it will use the y to determine whether reset root
return Res{ cmp_res ? y : x, y };
}
else {
// return nullptr
// -- for insert, don't create new node
// -- for emplace, drop created node
return Res{ pre.node_, nullptr };
}
}
Hint系列
标准库提供的Hint API有:1
2
3insert(const_iterator hint, T const& val)
insert(const_iterator hint, T&& val) // This isn't universal reference
emplace_hint(const_iterator hint, Args&&... args) // This is universal reference
先提个小问题:
为什么insert不需要重命名,而emplace需要呢?
1 | template<typename... Args> |
因为s不是const对象,所以end()返回的iterator而不是const_iterator,尽管iterator可以转换为const_iterator,但是相比模板实参推断不需要转换而言,它在重载决议中(overload resolution)是次一级的,所以重命名是最好的办法
Hint的逻辑异常简单,它只会试探提供的hint迭代器的前继和后继比较看能否插入hint的前面或后面,不行则调用insert/emplace()。
请读者自己试图理解以下代码,注释有部分说明。
1 | template<typename K, typename V, typename GK, typename CP, typename Alloc> |
相信读者在理解上述算法后,能够看懂下面接口,在此不再赘述1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133/**
* @brief Insert new node whose value is given value
* @param arg given value
* @return a pair value,
* the first value is iterator indicate inserted location
* and the second value is a boolean if insert successfully
*/
template<typename Arg>
pair<iterator, bool> InsertUnique(Arg&& arg) {
auto res = GetInsertUniquePos(GetKey()(arg));
if (res.second == nullptr) {
return TinySTL::make_pair(iterator(res.first), false);
}
return TinySTL::make_pair(
InsertAux(STL_FORWARD(Arg, arg), res.first, res.second),
true);
}
template<typename Arg>
iterator InsertEqual(Arg&& arg) {
auto res = GetInsertUniquePos(GetKey()(arg));
return InsertAux(STL_FORWARD(Arg, arg), res.first, res.second);
}
template<
typename II,
typename = Enable_if_t<is_input_iterator<II>::value>>
void InsertUnique(II first, II last) {
for (; first != last; ++first) {
InsertUnique(*first);
}
}
template<
typename II,
typename = Enable_if_t<is_input_iterator<II>::value>>
void InsertEqual(II first, II last) {
for (; first != last; ++first) {
InsertEqual(*first);
}
}
template<typename ...Args>
pair<iterator, bool> EmplaceUnique(Args&&... args) {
auto new_node = CreateNode(STL_FORWARD(Args, args)...);
STL_TRY {
auto res = GetInsertUniquePos(_Key(new_node));
assert(res.first == nullptr);
if (res.second) {
return make_pair(EmplaceAux(new_node, res.first, res.second), true);
} else {
DropNode(new_node);
return make_pair(iterator(res.first), false);
}
} CATCH_ALL {
DropNode(new_node);
RETHROW
}
}
template<typename ...Args>
iterator EmplaceEqual(Args&&... args) {
auto new_node = CreateNode(STL_FORWARD(Args, args)...);
STL_TRY {
auto res = GetInsertUniquePos(_Key(new_node));
assert(res.first == nullptr);
return EmplaceAux(new_node, res.first, res.second);
} CATCH_ALL {
DropNode(new_node);
RETHROW
}
}
template<typename Arg>
pair<iterator, bool> InsertHintUnique(const_iterator pos, Arg&& arg) {
auto res = GetInsertUniqueHintPos(pos, GetKey()(arg));
if (res.second == nullptr) {
return make_pair(iterator(res.first), false);
}
return make_pair(
InsertAux(STL_FORWARD(Arg, arg), res.first, res.second),
true);
}
template<typename Arg>
iterator InsertHintEqual(const_iterator pos, Arg&& arg) {
auto res = GetInsertEqualHintPos(pos, GetKey()(arg));
return InsertAux(STL_FORWARD(Arg, arg), res.first, res.second);
}
template<typename ...Args>
pair<iterator, bool> EmplaceHintUnique(
const_iterator pos,
Args&&... args) {
auto new_node = CreateNode(STL_FORWARD(Args, args)...);
auto res = GetInsertUniqueHintPos(pos, _key(new_node));
if (res.second == nullptr) {
return make_pair(res.first, false);
}
STL_TRY {
return make_pair(
EmplaceAux(new_node, res.first, res.second),
true);
} CATCH_ALL {
DropNode(new_node);
RETHROW
}
}
template<typename ...Args>
iterator EmplaceHintEqual(
const_iterator pos,
Args&&... args) {
auto new_node = CreateNode(STL_FORWARD(Args, args)...);
auto res = GetInsertEqualHintPos(pos, _Key(new_node));
STL_TRY {
return InsertAux(new_node, res.first, res.second);
} CATCH_ALL {
DropNode(new_node);
RETHROW
}
}
rbtree的删除接口
erase共有两个接口:
- erase():删除单个元素
- clear():删除整棵树
它们采取的算法各不一样,下面开始展开
删除单个节点
erase的理论在那篇博文也提到了,主要是依赖于brother和它的child,具体细节这里不展开,算法如下:
由于erase不需要用到value字段,因此整个算法实现都可以写在源文件(.cc)中
1 | /** |
BST的删除算法在BST的博客中也提过,这里需要把双黑点和双黑点的parent清出来调用上面这个接口,不再赘述。
1 | /** |
删除整棵树
如果采取范围删除整个树,那么是灾难性的,
尽管我可以每次获取begin花费$O(1)$,但是整个删除也需要$O(nlgn)$
STL采用top-down的删除方式使得时间复杂度降到$O(lg^{2}n)$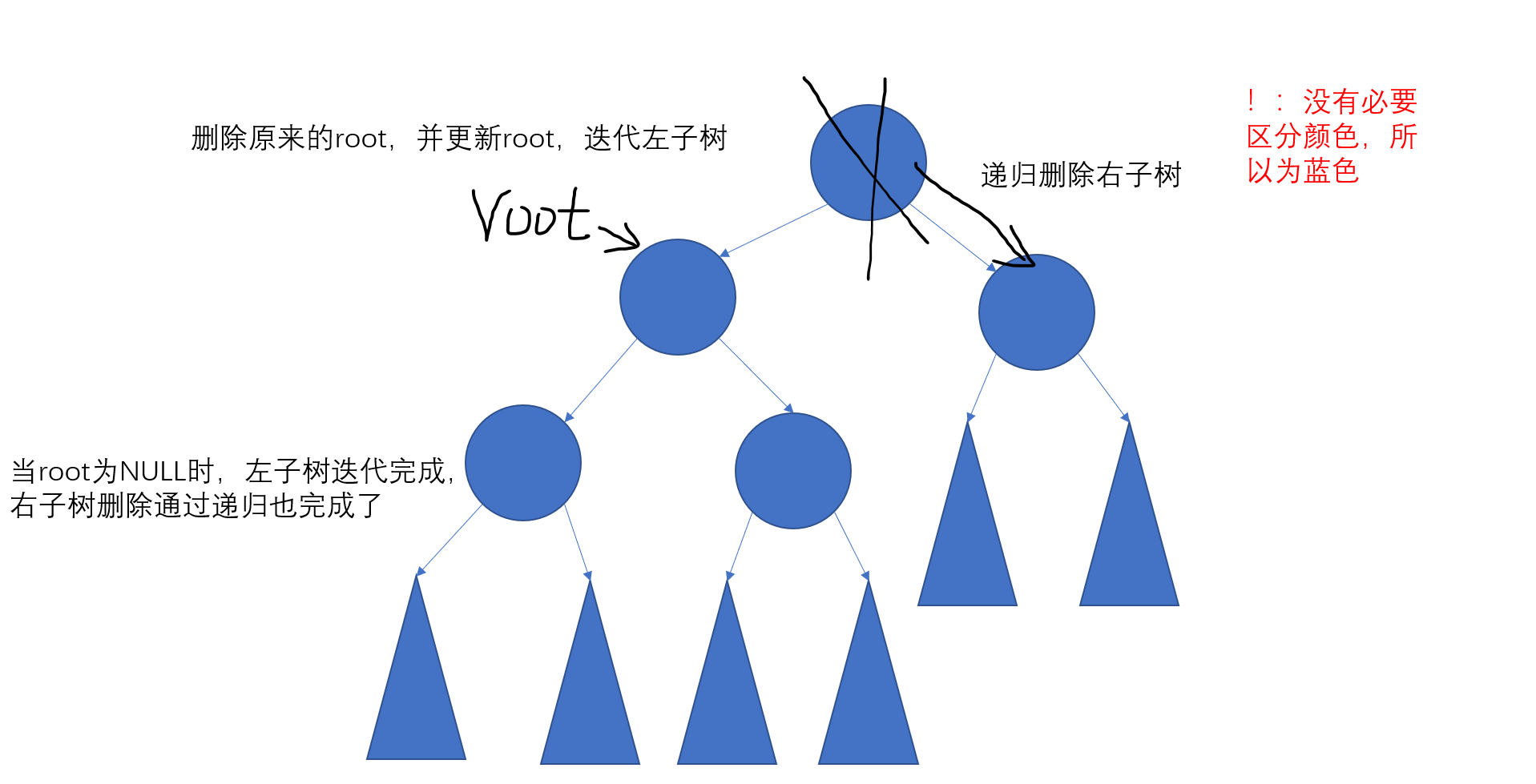
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template<typename K, typename V, typename GK, typename CP, typename Alloc>
void RBTree<K, V, GK, CP, Alloc>::Erase(LinkType root) noexcept {
//no rebalance
while(root){
// erase right subtree on the left child line
Erase(Right(root));
auto y = Left(root);
DropNode(root);
root = y;
}
}
void clear() noexcept {
Erase(static_cast<LinkType>(Root()));
// reset header...
}
rbtree的拷贝
移动是没什么好讲的,我们主要讲下rbtree的拷贝接口,它是拷贝构造函数(copy constructor)和拷贝赋值运算符(copy assignment operator)的具体实现
拷贝赋值的时候,已有的树的节点如果多于参数的树(令它为other),那么我们可以复用相当于other.size()个节点进行析构和重构造而不需要销毁它(省去了free或::operator delete的开销),然后销毁多余的节点(this->size() - other.size())。
如果少于other.size(),那么应当复用所有节点,并创建other.size()-this->size()个新节点。
这意味着什么?意味着我们需要采取两种alloc policy
- PlainAlloc,简单的alloc的wrapper
- ReuseOrAlloc,当有节点可复用时,返回该节点,不然调用PlainAlloc进行构造
Reuse的逻辑如下图所示
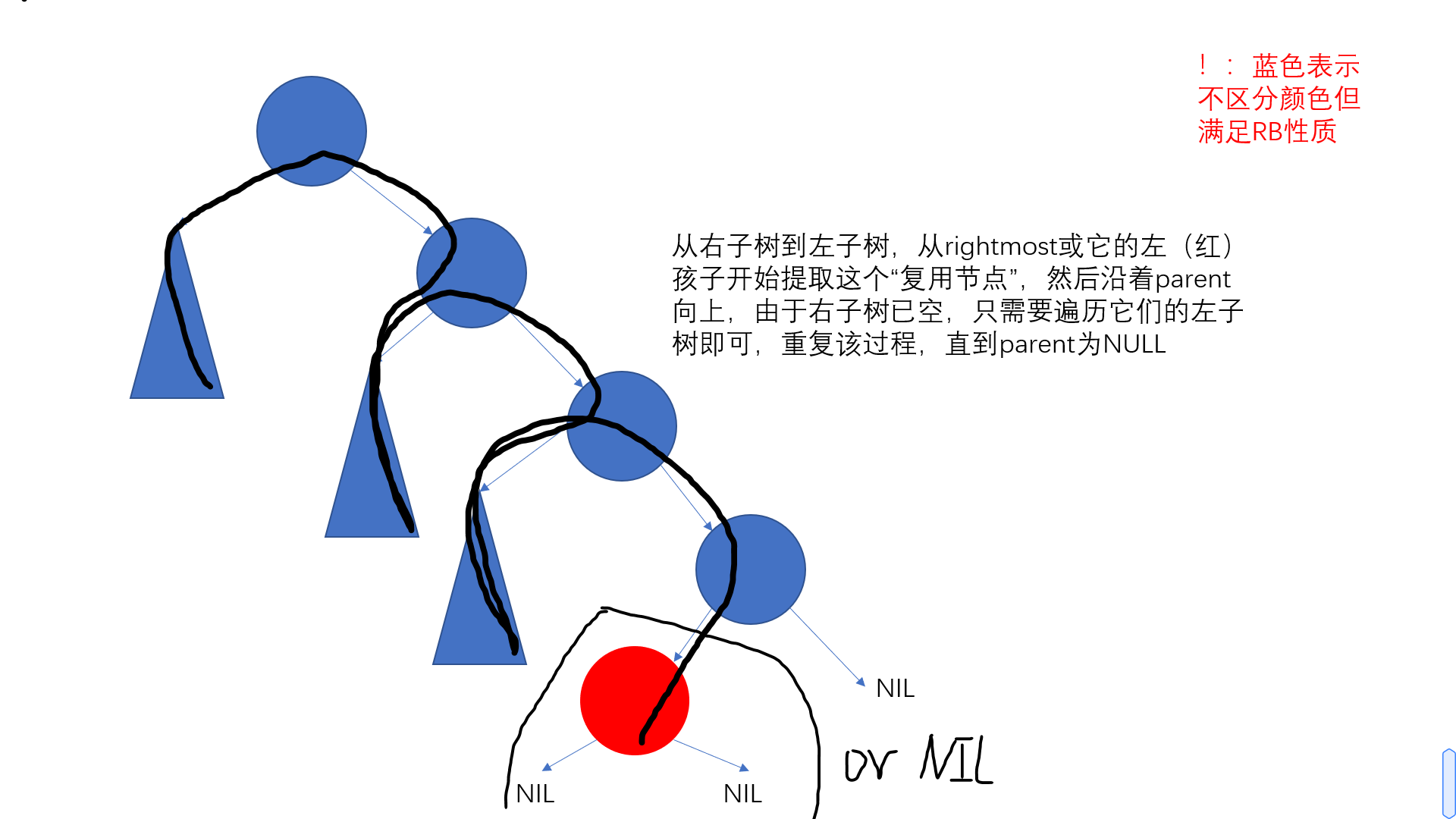
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88/**
* @class ReuseOrAlloc
* @brief
* reuse original nodes, destroy and reconstruct
* when no nodes, plain alloc
*/
struct ReuseOrAlloc : noncopyable {
public:
explicit ReuseOrAlloc(RBTree& rbtree)
: rbtree_{ rbtree }
, node_{ rbtree.RightMost() }
, root_{ rbtree.Root() }
{
if (root_) {
// for Extract()
root_->parent = nullptr;
// node is rightmost, so left subtree
// have a red child at most
if (node_->left) {
node_ = node_->left;
}
} else {
// if root_ is NULL, node_ is header
node_ = nullptr;
}
}
~ReuseOrAlloc() noexcept {
// if root_ is not NULL, there are some nodes can't be reused
// we can only destroy and free them
if (root_) {
rbtree_.Erase(static_cast<LinkType>(root_));
}
}
template<typename... Args>
LinkType operator()(Args&&... args) noexcept {
auto reuse_node = static_cast<LinkType>(Extract());
if (reuse_node) {
rbtree_.DestroyNode(reuse_node);
rbtree_.ConstructNode(reuse_node, STL_FORWARD(Args, args...)...);
return reuse_node;
} else {
return rbtree_.CreateNode(STL_FORWARD(Args, args)...);
}
}
private:
BasePtr Extract() noexcept {
if (node_) {
auto reuse_node = node_;
node_ = reuse_node->parent;
if (node_) {
if (node_->right == reuse_node) {
node_->right = nullptr;
if (node_->left) {
node_ = node_->left;
while (node_->right) {
node_ = node_->right;
}
if (node_->left) {
node_ = node_->left;
}
}
} else { // end if node->right == reuse_node
node_->left = nullptr;
}
} else { // end if node_
// reuse_node parent is NULL, set root_ to NULL
// to avoid destroy root in top-down in destructor
root_ = nullptr;
}
return reuse_node;
}
return nullptr;
}
RBTree& rbtree_;
BasePtr node_;
BasePtr root_;
};
然后就是copy的具体实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33template<typename K, typename V, typename GK, typename CP, typename Alloc>
template<typename Policy>
typename RBTree<K, V, GK, CP, Alloc>::LinkType
RBTree<K, V, GK, CP, Alloc>::Copy(LinkType x, BasePtr p, Policy& policy){
auto top = CloneNode(Value(x), policy);
// top->parent may be resetd to NULL in ReuseAlloc
top->parent = p;
STL_TRY{
//because rbtree is also a binary tree, so copy one direction in recursion
//just handle one direction
if(x->right)
top->right = Copy(Right(x), top, policy);
p = top;
x = Left(x);
// x
while(x){
auto y = CloneNode(Value(x), policy);
p->left = y;
y->parent = p;
if(x->right)
y->right = Copy(Right(x), y, policy);
p = y;
x = Left(x);
}
} CATCH_ALL {
erase(top);
}
return top;
}
思路同Erase(),这里注意到了其实有重复代码,那是为了处理异常妥协的
接口则将要拷贝的树传进来,
而且注意,传进来的树不能是空树,所以我们需要处理一下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template<typename Policy>
void Copy(RBTree const& rb, Policy& policy){
if(rb.Root()) {
Root() = Copy(
static_cast<LinkType>(const_cast<BasePtr>(rb.Root())),
Header(),
policy);
LeftMost() = Minimum(Root());
RightMost() = Maximum(Root());
impl_.node_count = rb.impl_.node_count;
} else {
clear();
impl_.Reset();
}
}
然后拷贝构造函数和拷贝赋值运算符重载根据alloc policy调用其接口便可1
2
3
4
5
6
7
8
9
10
11
12
13RBTree(RBTree const& rhs) {
PlainAlloc policy(*this);
Copy(rhs, policy);
}
RBTree& operator=(RBTree const& rhs){
if(this != &rhs){
ReuseOrAlloc policy(*this);
Copy(rhs, policy);
}
return *this;
}
尾声
以上代码取自于本人的TinySTL,可以点击以下链接:
stl_tree.h
stl_tree.cc
(代码可能很多没有对齐,是因为编辑器设置问题,不建议在GitHub上看,你可以clone或fork)
插入,删除,查找,拷贝的单元测试(gtest)和benchmark在test文件夹亦可找到,内存泄漏问题通过valgrind检测应该是没有问题。
至于性能,基本上可以达到标准库的90%(release模式),debug模式的话是比标准库快的(毕竟没有什么包袱)。原因可能是rebalance算法优化过,毕竟STL采用的理论也是来源于CLRS(算法导论)。这个暂且不论。
此文可能需要再补充或修改错误。






