红黑树

红黑树保证两颗子树之间高度不会相差两倍以上，因此是（红黑）“近似平衡”（黑节点是完美平衡）的

红黑树满足以下性质（约定称为RB性质）：

Every node either red or black
The root and leaves(NIL ‘s)are black
If a node is red,then its parent is black
All simple paths from any node $x$ to a descendant leaf have the same number of black nodes =black-height($x$) or bh($x$)

（注意$bh(x)$不包含$x$本身，即本身是黑节点不记数，否则黑高和等价2-3-4树的高度不等）

我们称leaf为external node，而其他保存键值的为internal node

这里的$NIL$并不是用空指针表示，而是用一个实际的节点$T.nil$表示，颜色为BLACK，其他随意。用作哨兵处理边界条件：空指针没有颜色，而$T.nil$有（比如下面插入时，假如uncle是叶子的话，那么就必须要考察其颜色）。不设成RED是因为出现两个连续红节点的情况会增多（或概率增大），而这违反了性质3。同时为了节省空间，叶节点和根节点的父节点都用NIL表示。

红黑树示意图（实际上根节点的父节点也是NIL，省去了）：

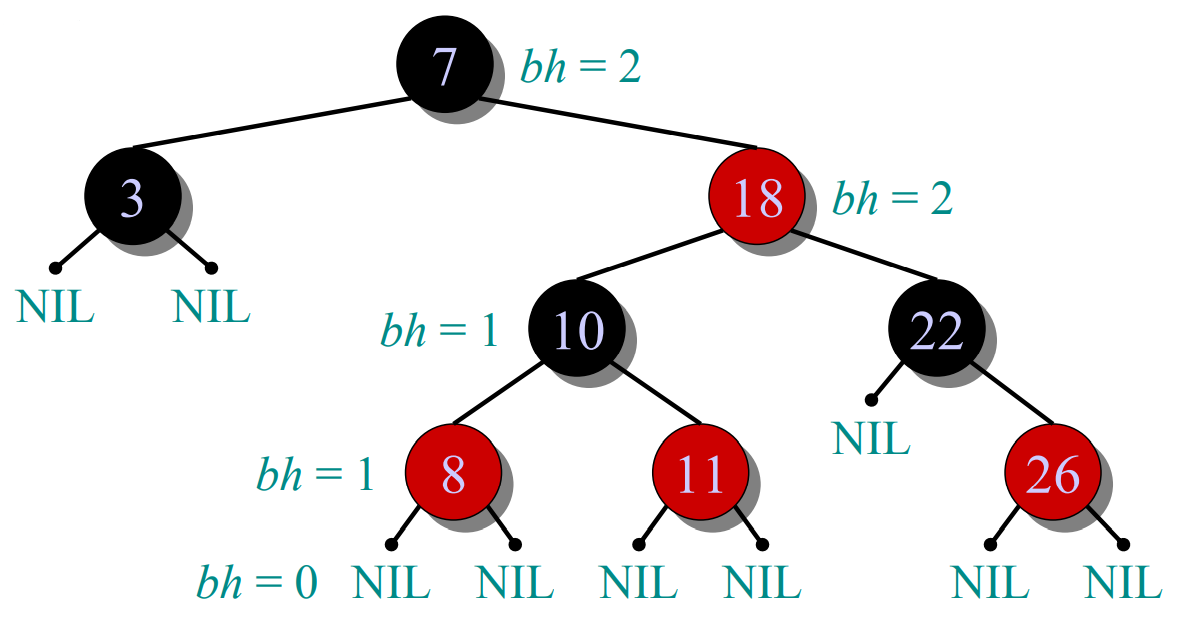
为了说明红黑树的优越性引入一条定理：

Theorem

A red-black tree with n keys has height

$h \le 2 lg(n+1)$

这里我们用2-3-4树来证明该定理（实际上，红黑树是2-3-4的等价实现只不过两叉+染色，因为2-3-4有些编程语言不好实现）

(PS：也可用数学归纳法证明该定理，具体参考CLRS ch13.1 page 309)

先简单介绍下2-3-4树的特点：

2表示该节点存储一个key，有两个孩子，3和4类推

我们将一个红节点与它的黑父节点结合(吸收)成为一个新节点，这样所有节点都成为黑节点了，从根节点到叶子的路径长度就是黑高，即该树的高度

2节点——1黑
3节点——1黑1红
4节点——1黑2红

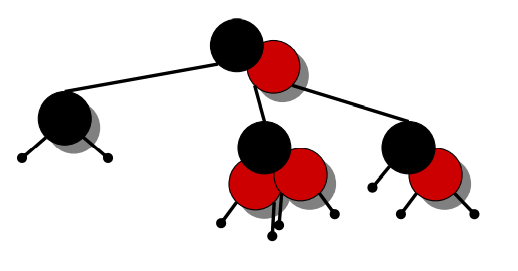
等价图：

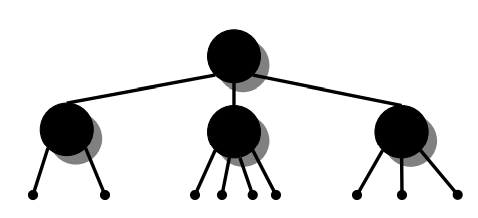
实际上你会发现等价的2-3-4树是完美平衡，因为高度差为0（由性质4保证）。

我们设红黑树高度为$h$，等价2-3-4树高度为$h’$，内部节点数$n$，外部节点数为$m$，叶子节点数为$leafs$,

因为一个红黑树也是二叉树，一个节点分出两个孩子，因此$m=n+1$并不难理解(前提是所有节点都有两个孩子，而红黑树满足)

我们用数学归纳法也可以证明：

当$m=1$时，$n=2=m+1$，命题成立
假设当$m=k>1$时，$m=n+1$成立
当$m=k+1$时，加一个内部节点需要增加一个外部节点，故$m=m_k+1=n_k+2=n+1$ $\blacksquare$

而在2-3-4中，叶子节点数没变，接下来我们来决定叶子节点数和高度之间的关系

如果都是二叉，那么叶子节点数=$2^{h’}$
如果都是四叉，那么叶子节点数=$4^{h’}$

因此得到不等式

$2^{h'} \le leafs=n+1 \le 4^{h'}$

取左边的部分不等式，得到$h’ \le lg(n+1)$

由红黑树性质3可得知：红节点的父母必须是黑节点，而黑节点的父母不做限制，即不允许连续两个红节点出现，红节点总数至多为一半

所以$h’=bh(T.root) \ge \frac{h}{2}$

所以$h \le 2lg(n+1)$

一个红黑树的高度最高为$O(lgn)$，保证了BST的所有操作为$O(h)=O(lgn)$

同时，由这个定理的证明可以知晓RB4个性质的必要性：

性质1是性质3的铺垫
性质2减少了插入时连续红节点的出现概率
性质3保证了红色最多的时候是红黑相间，此时黑高最小为高的一半
性质4保证了黑高一致，即转换为等价2-3-4树时的高度

接下来只讲解红黑树的两个操作：INSERT和DELETE，因为其他的BST已实现过

ROTATION

因为INSERT和DELETE都改变了树的结构，可能会违反RB性质，因此需要考虑再染色（recolor）和改变指针结构

而改变指针结构就通过$RATATION$操作实现，一般译作“旋转”

旋转的意义在于只改变一个节点和它的孩子的关系而不影响树的其他结构，同样，它也不会破坏BST性质

旋转实际上是绕一个“主轴”（pivot）成90°角度旋转，子树相对位置没变（很多博客对于旋转的描述简直没法看，简单的复杂化）

而且你会发现右旋的话，主轴在左边，左旋反之

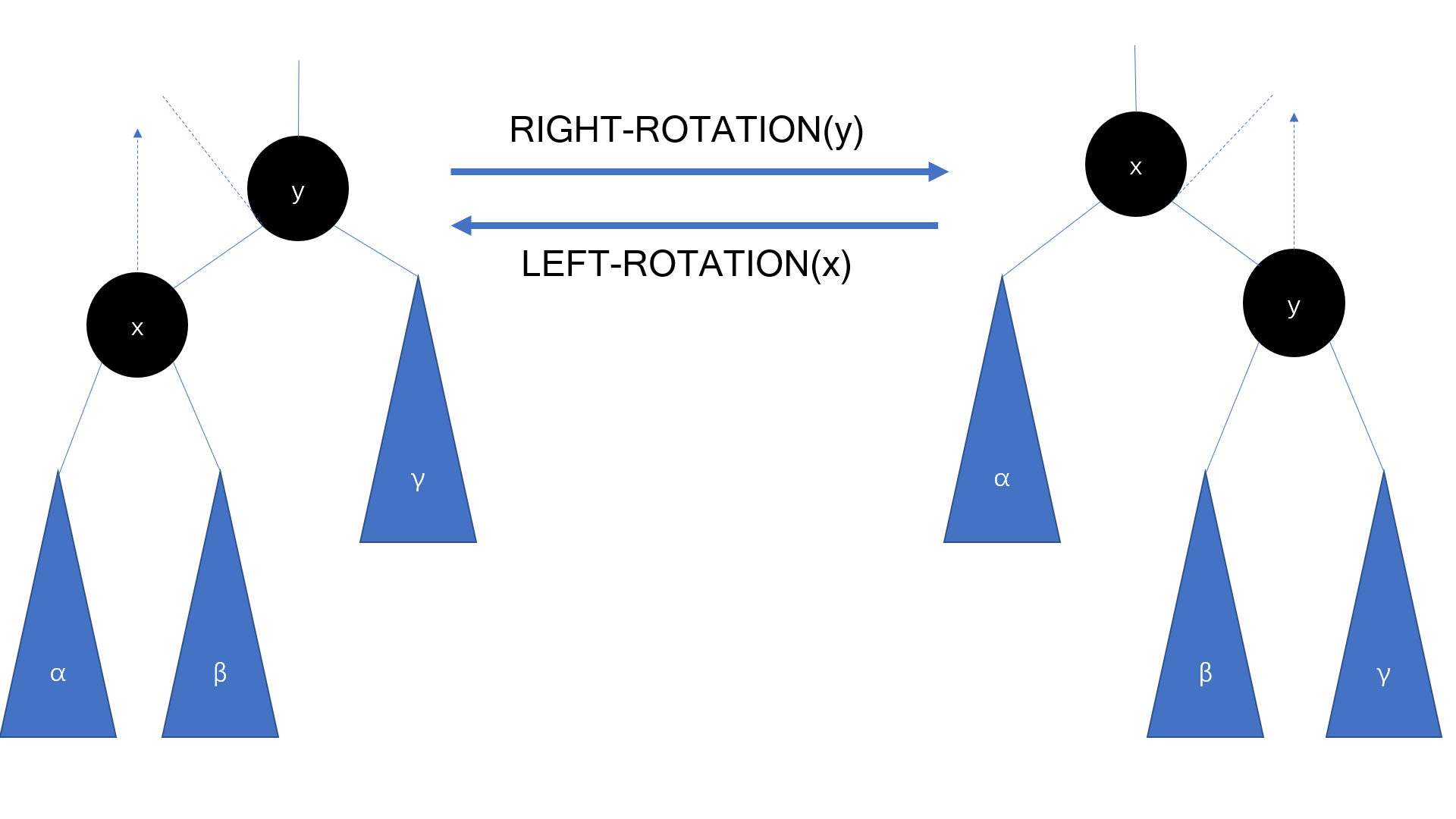旋转操作使得原来的孩子成为新的根节点，而原来的根节点变成孩子并接手原来孩子的一个子树。通过该操作，还可能减小子树间高度的相差，接近严格平衡（INSERT有体现）。

根据以上信息，我们可以写出左旋的伪代码：

LEFT-ROTATION(T,x)
y ← x.right
x.right ← y.left		//转交子树

if y.left ≠ NIL
 then y.left.p ← x		//重定向y.left’s parents

y.p ← x.p				//链接x.p和y
if x.p = NIL
 then T.root ← y
 elseif x.p.right = x
  then x.p.right ← y
  else
   x.p.left ← y
  
y.left ← x				//链接x和y
x.p ← y

右旋伪代码（习题13.2-1):

RIGHT-ROTATION(T,y)
x ← y.left
y.left ← x.right

if x.right ≠ NIL
 then x.right.p ← y
 
x.p ← y.p
if y.p = NIL
 then T.root ← x
 elseif y.p.right = y
  then y.p.right ← x
  else
   y.p.left ← x
   
x.right ← y
y.p ← x

INSERT

IDEA:

Insert $x$ in tree.Color x red.Only red-black property 3 might be violated.Move the violation up the tree by recloring until it can be fixed with rotations and recoloring

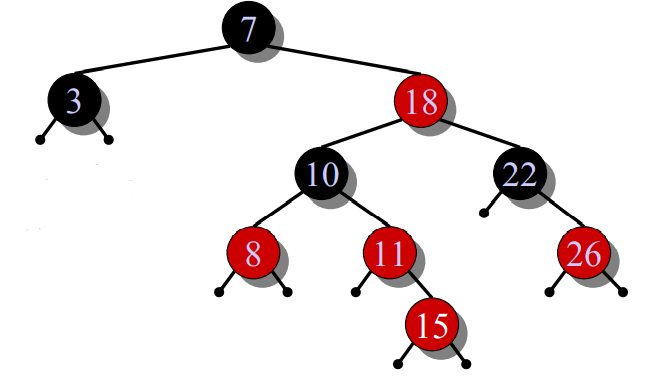
流程讲解

插入一个红节点，结果出现了连续红节点，违反了RB性质3，我们会将这个破坏上移两个层次给它的grandpa，直到可以通过旋转和染色终止循环。（PS：当出现两个红节点时，grandpa一定存在）

首先，明确为什么要插入红节点？
因为RB性质4必须保证黑高一致，而插入黑节点就破坏了性质4。

（假设以下示意图中其他子树均满足RB性质，设插入点为$x$）

CASE 1:$x$’s uncle is red

现在有两个连续红节点，第一直觉就是将parent染黑，那么就能维护性质3，但是性质4被破坏了，如果想要维护性质4的话，需要同步parent与uncle（对称节点），这样可以使得两边黑高一致，同时将grandpa（黑）染红，由于grandpa仍可能失衡，此时就需要更新失衡节点（即实现“破坏上移”），直到可以通过recolor和ratation解决，这就是用到uncle调节平衡的原因。

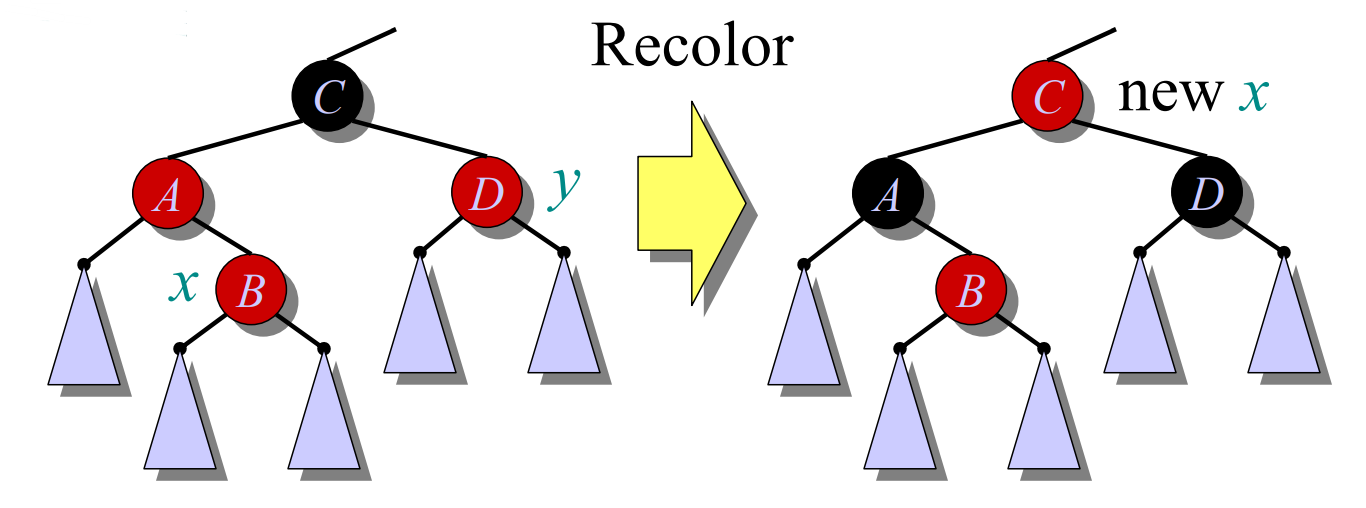
但是这个循环什么时候终止呢？

一直上升。由于是以两个层次单位进行，若$new \ x$为$T.root$的孩子，因为根节点是黑的，已实现平衡；若$new \ x$为$T.root$，则将两个孩子染黑，$new \ x$虽然染红了，但是特殊情况特殊处理，这种情况会再度染黑，这样，即使黑高增1，性质4也没有被破坏，而性质3也得以维护
uncle为黑。进入CASE2或CASE3

下图是插入15时的处理：

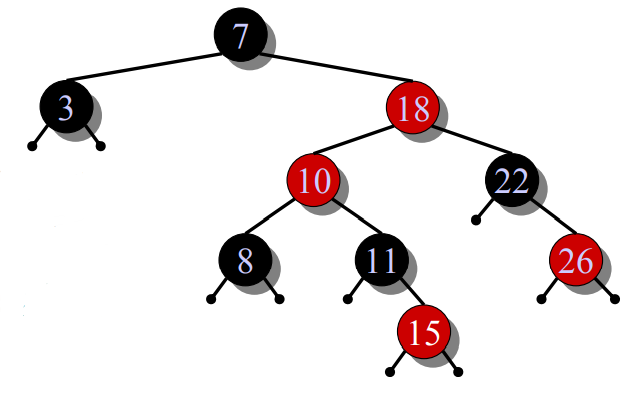
现在考虑了uncle为红的修复情况，为了覆盖所有情况，我们还需要考虑uncle为黑的情况，并提出解决方案:

我们仍然考虑染黑parent，但是会破坏性质4，因为uncle是黑色，我们可以染红grandpa而不破坏性质3，此时只有右子树黑高较左子树少1，那么把红根节点下移，黑parent上移成为新的根节点，即绕D左旋，就可以恢复性质4(而且还减少了高度差）

那么问题在于重染色和旋转后会不会又破坏性质，我们假定新插入节点和parent的关系未知，那么旋转之后的图如下所示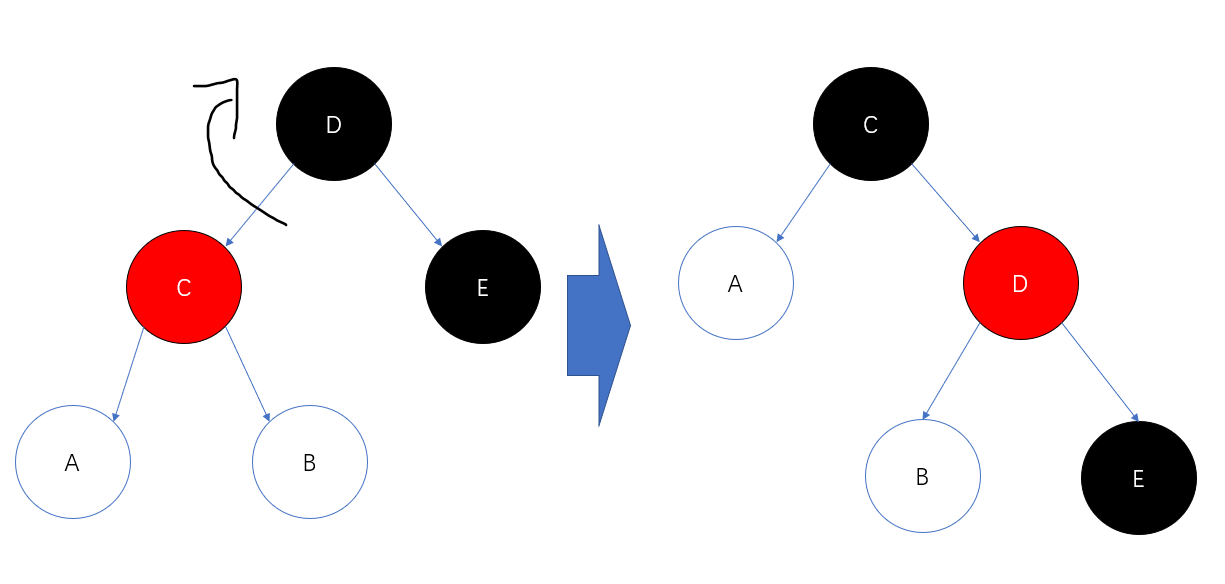

可以确认到黑高没问题，唯一不可测的就是红节点究竟是A还是B？如果为B会继续破坏性质3，所以新插入节点如果为左节点会最好，如果为右节点的话，可以通过旋转转化，这就是case2和case3的来源。

CASE 2:$x$’s uncle is black and $x$ is a right child

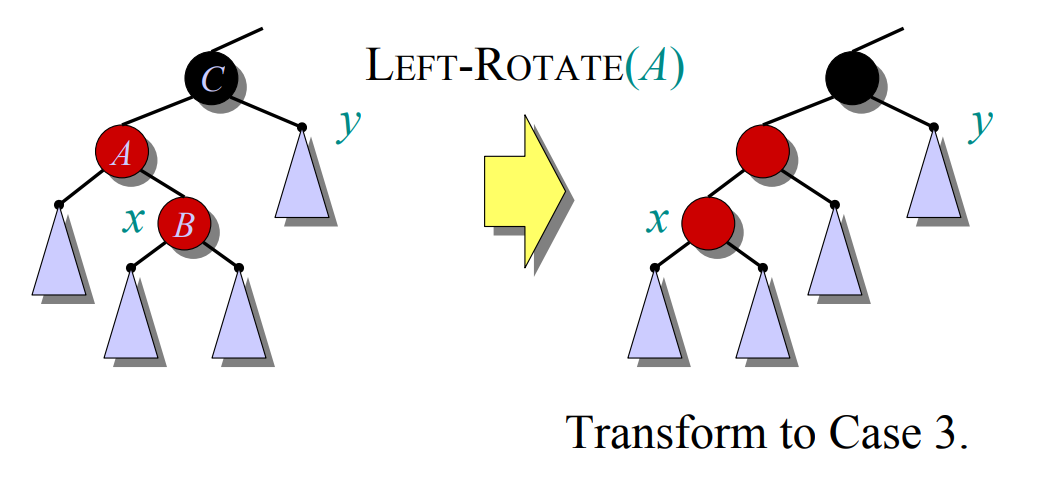
CASE 3：$x$’s uncle is black and $x$ is a left child

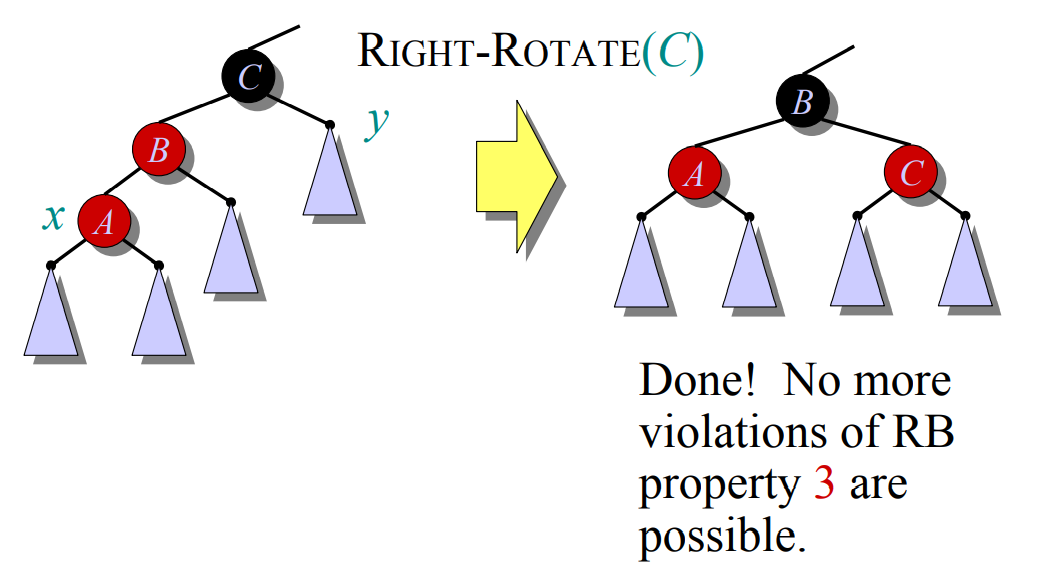
上面那个例子的话，过程就是

RIGHT-ROTATION(18)，使黑-红-红在一条直线上

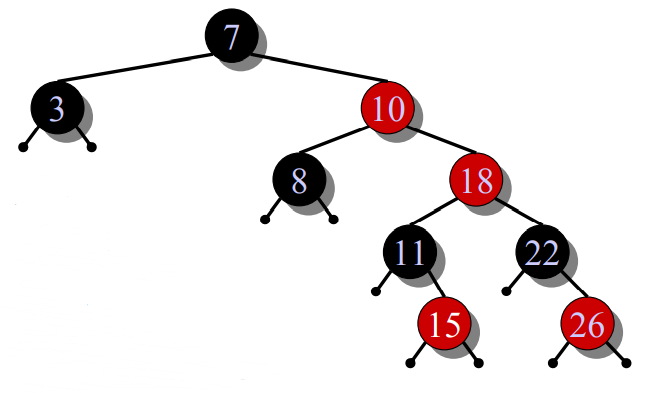
LEFT-ROTATION(7)，重染色：原根节点染红，新根节点染黑

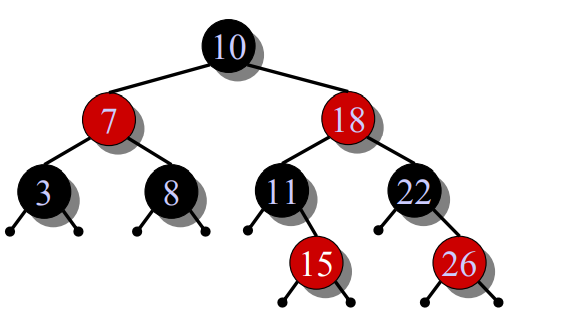
实际上根据uncle与插入节点的相对位置，可以分为两种位置，而一种位置有3种情形，上面提到的CASE1、CASE2、CASE3是grandpa的右孩子是uncle的情形，而grandpa的左孩子为uncle时，也有三种情形，和CASE 1~3 完全对称

有了这些铺垫，伪码如下：

RB-INSERT(T,z)
y ← T.nil
x ← T.root

while x ≠ T.nil
 do y ← x 
  if z.key < x.key
   then x ← x.left
   else
    x ← x.right

z.p ← y
if y = T.nil
 then T.root ← z
 elseif z.key < y.key
  then y.left ← z
  else
   y.right ← z
   
z.right ← T.nil
z.left ← T.nil
z.color ← RED
RB-INSERT-FIXUP（T,z)

RB-INSERT-FIXUP(T,z)
while z.p.color = RED
 do if z.p.p.left = z.p
     then y ← z.p.p.right
      if y.color =  RED				//<CASE1>
       then
        y.color ← BLACK
        z.p.color ← BLACK
        z.p.p.color ← RED
        z ← z.p.p
      else if z.p.right = z			//<CASE2>
            then
             z ← z.p
             LEFT-ROTATION(T,z)
           z.p.color ← BLACK		//<CASE3>
           z.p.p.color ← RED
           RIGHT-ROTATION(T,z.p.p)
    else
     <with "left" and "right" swapped>
T.root.color ← BLACK    //RB property 2

时间复杂度

首先，我们像一般BST一样插入一个节点，时间复杂度为$O(h)=O(lgn)$

只有CASE1才会循环，每次上升两个水平，而树高为$O(lgn)$，故$INSERT-FIXUP$时间复杂度为$O(lgn)$

故整个插入操作时间复杂度为$O(lgn)$

DELETE

TARANSPLANT

因为$T.nil$是一个确实的节点，而不是NIL，因此$\text{RB-TRANSPLANT}$稍微有一点不同：

而且注意，链接parents不需要检测替代节点是否为$T.nil$，这个很关键，因为后面删除操作很可能$T.nil$上位，那么就必须要知道$T.nil$的parents，一般$T.nil$除了color是black外，其他的都是任意的

RB-TRANSPLANT(T,u,v)
if u.p = T.nil
 then T.root ← v
 elseif u.p.left = u
  then u.p.left ← v
  else
   u.p.right ← v
   
v.p ← u.p //无条件链接parents

为讲解方便，我们约定

$y$表示
- 将删除节点（one child）
- 将删除节点的后继（two child）（必然在右子树，因为此时拥有两个孩子）
因为$y$的移去可能导致破坏RB性质，因此需要用一个变量$y-original-color$存储$y$原来的颜色。
因为$y.right$会占据$y$的原位置，我们用$x$来表示这个节点（以下两种情况是讨论two child）（one child亦用$x$表示$y.right$）
- 如果 $y.p \ne z$，因为$y.p$不会被移去，因此$x.p=y.p$
- 如果 $y.p =z$，则直接$x.p=y$
如果$y-original-color=RED$，那么不需要维护红黑树，因为不会有任何性质被破坏
1. 既然是红节点，自然黑高不会改变，因此性质4维持
2. 根节点必然是黑的。因为如果$y$颜色为红色，它是不可能成为根节点的，性质2维持
3. 不可能出现连续两个红节点。因为红节点的父母必然是黑节点，其孩子也为黑节点，因此即使$y$移动，原来的位置被黑节点也不会出现任何问题。性质3维持

所以$y-original-color=BLACK$才是我们应该关注的问题。RB性质几乎都可能被破坏：

性质2：如果$y$是根节点，右孩子为红节点，右孩子取代$y$，违反性质2
性质3：$x$ 和 $y.p$ 都是红的，违反性质3
性质4：这个是最显然的，将黑节点一拿，黑高就减一了，那么该节点($y$)之前的祖先均违反性质4

性质2好维护，只要调整的时候将根节点顺便染黑就行了（以下CASE2和CASE4处理了，自己尝试证明一下）

性质3也好维护，直接把$x$染黑就行了，因为原来$y$在的时候，就没破坏任何性质，恢复原状罢了（同时，你会发现，当$y.p$的另一个孩子成为它的兄弟时，它是唯一的孩子且是红的）

那么（最难的）性质4，怎么维护呢？转化多出来的黑色！

因为$x$会占据$y$的原位置，我们可以给$x$添加一个“额外”的黑色（extra black），这样性质4就没破坏

但是这个“额外”的黑色给$color$吗？这样就违反了性质1，$x$成为了黑/红节点以外的节点，但是我们可以给节点本身赋予黑色（可能有点抽象）

我们约定如果$x$本身是红色，则加上“额外”的黑色称为红-黑点（red-and-black node)，本身是黑色，则称为双黑点（doubly black node）

（P.S. 如果是one child，那么$x$必为红黑点，因此操作是trivial的，no child亦是如此，所以真正需要处理的是two child）

但是实际上，这个“额外”的黑色并不存在，因此我们必须想办法去掉它

我们会设计一个循环，其目的是将黑色节点上移（和插入的IDEA是一致的），直到

$x$指向红-黑点，我们将它染成黑色以去除extra black（如果$x$到达根节点，则此时将兄弟染红）
$x$的兄弟右孩子为红（或左红右黑），在这种情形，可以通过合适的旋转和再染色去除extra black

之所以考虑用brother去除extra black，是因为我们需要维护性质4：保证两边的黑高一致，这边去除的话，另外一边也必须同步（所以你会理解为什么case1要先把red brother转化为black brother）,这个其实和插入的IDEA是一样的

在整个循环过程中，$x$是双黑点，我们维护一个节点$w$来表示$x$的兄弟。该兄弟不可能为$T.nil$，否则$x.p$到$x$的路径长度比$x.p$到$w$的长度要长

所以不要担心兄弟会是外部节点（我就钻了进去结果没意识到兄弟根本不可能是叶子）

KEY IDEA

In each case,the transformation applied preserves the number of black nodes(including $x$’s extra black) from(and including) the root of the subtree shown to each of the subtrees $\alpha,\beta,…,\zeta$

根据这个IDEA，我们用

$c(color)= \begin{cases} 0 \ if \ color=RED(including \ red-black ) \ &\\ 1 \ if \ color=BLACK(including \ doubly \ black) \ &\\ \end{cases}$

作为子树根的计数，我们需要保证变换前后（包括）子树根到各子树的黑节点数是相等的

以下变换都是基于该思想（子树略掉了，反正从左到右顺序不会变）

情形分析

CASE 1:$w$ is red

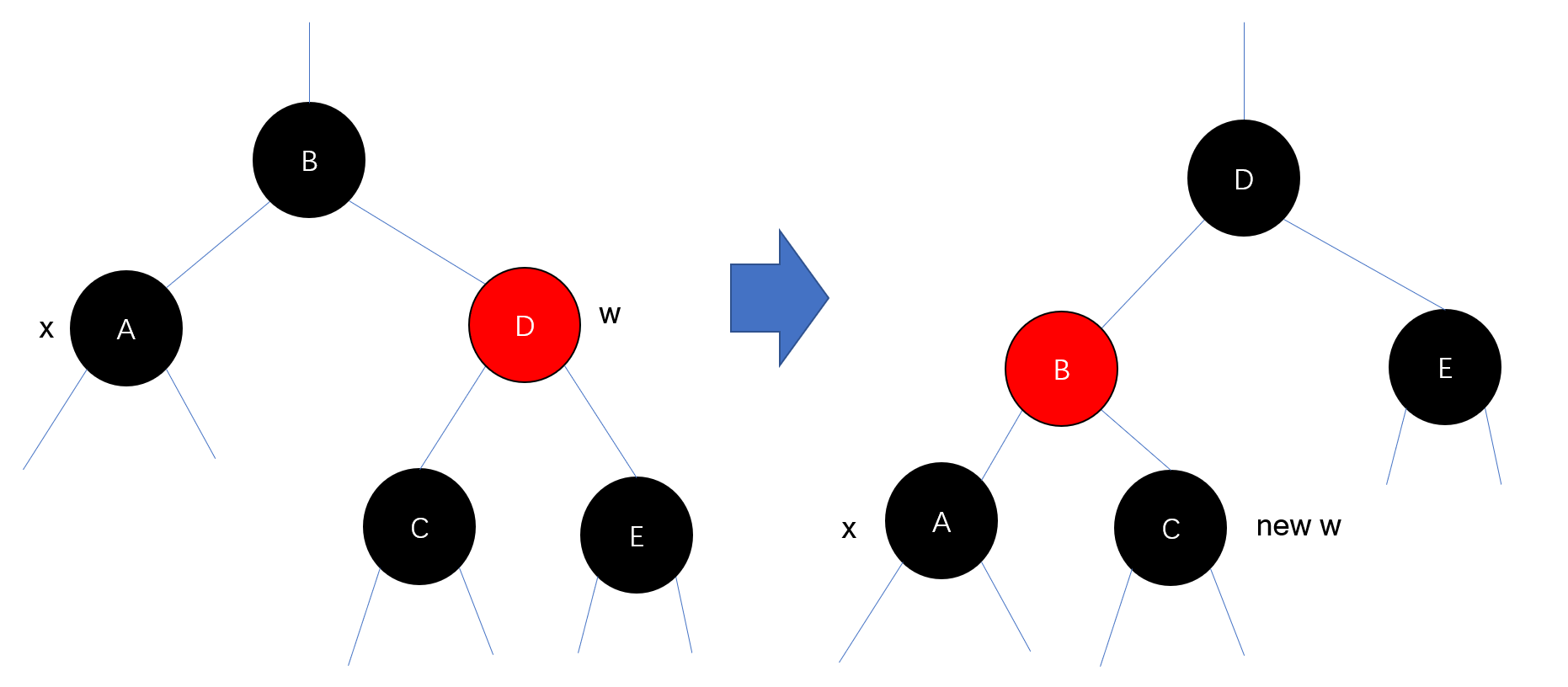
注意变换前后，根节点到子树的黑节点数不变，假设A的左孩子为$\alpha$，那么B到它的黑节点数为3，变换后依然为3（因为B染红了）

我们可以把右边的子树情况对称变换成左边，$x$随着下移，这样兄弟就是黑节点了，而且因为对称，自然前后黑节点数不变。

该情形只是用来过渡的：将红兄弟转变为黑兄弟，因为只有黑兄弟才能剥离extra black，

CASE2是通过染红兄弟，将extra black给了parents
CASE4是通过将黑色兄弟转变成自己的父母而去除了extra black

根据黑兄弟的孩子区分得到CASE2，CASE3，CASE4

CASE 2:$w$ is black ,$w.left$ and $w.right$ is black

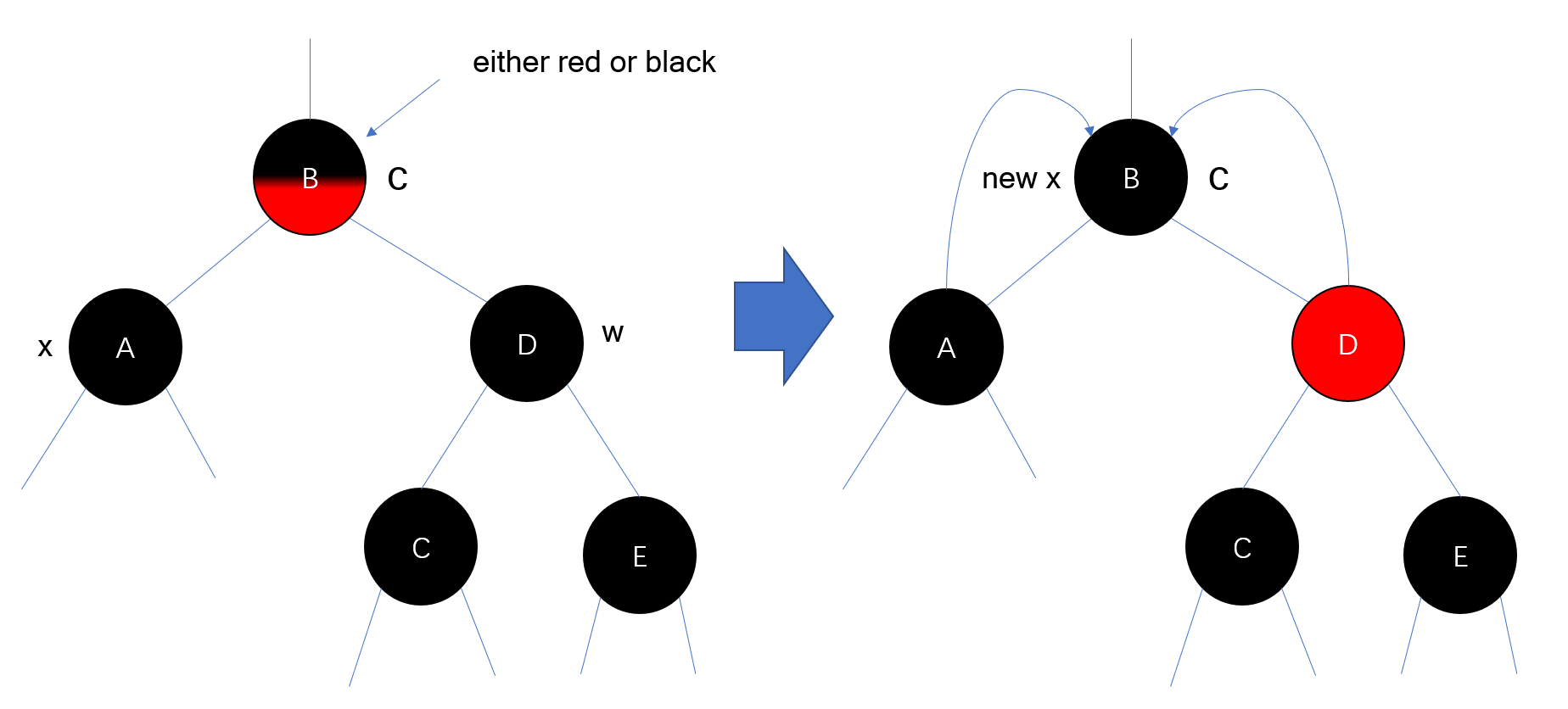
该case类似于insert的case1，通过去除两边的black将破坏上移。
之所以需要两个child为黑，是因为需要维护性质3。

因为$x$和$w$都是黑色，我们可以同时去除它们的黑色给$x.p$，如果$x.p=RED$（比如CASE1$\rightarrow$CASE2)，就可以退出循环然后将其染黑达成去除extra black的目的，性质4得到了维持；如果$x.p=BLACK$，$new \ x$是双黑点，则继续循环（如上所述，我们这里是将extra black赋予给parents本身）

你可能会说：如果这条路径全部都是黑节点咋办，遇不到红节点，而根节点是黑的，已经上不去了啊？

注意这种极端情况，一般情况，我们是通过移除extra black给父节点，直到遇到红节点，将它染黑。

但是根节点是$new \ x$的话，已经上不去了，但也没有上去的必要了，根节点是双黑点，但是extra black已经吐不出来了，因为它的parents是$T.nil$，那就不吐了，直接将兄弟染红，使得黑高减1但是黑高仍相等，并没有违反性质4，因此是合理的（当然遇到红节点最好，直接退出循环），你可以试着画一颗全黑树，就是可以一直上升最终把根节点的另一个孩子染红了（网上博客有人还评论全黑树怎么删，写算法都不考虑边界条件的吗）

此时还剩下未处理情形有：

left is red, right is black
left is black, right is red
left is red, right is red

我们假设黑兄弟的孩子颜色除了不允许双黑之外未知，此时我们已经无法剥离兄弟的黑色了，因为会破坏性质3，我们改变思路，通过旋转使得到从根节点到双黑点的路径上黑节点增多，即将黑色转让给parent，通过B的左旋可以轻松做到，然后通过重染色维护性质3和性质4即可。
如下图所示：

（白色表示要么是黑要么是红）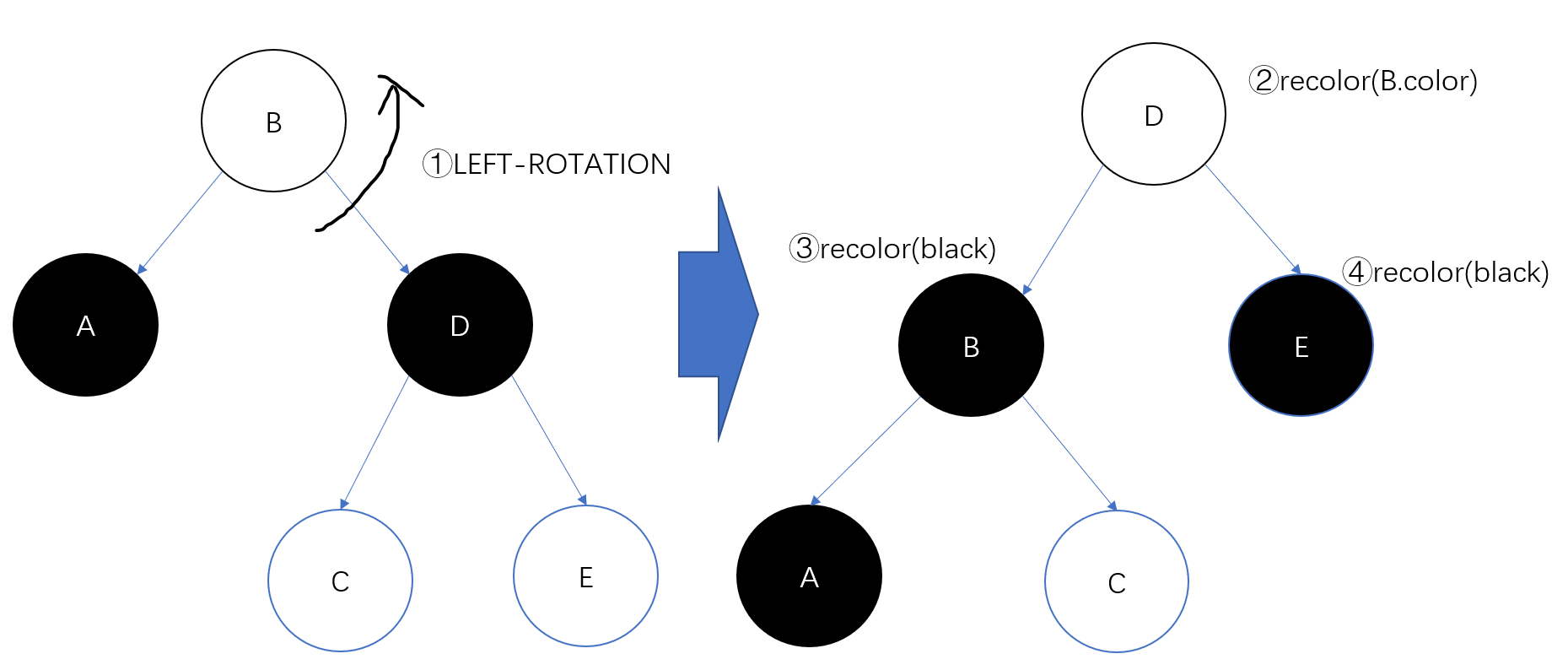

但是有个问题，如果E本身就是黑色，那么性质4仍是被破坏的，因此当右孩子为黑色的时候，我们需要旋转将它转化为右孩子为红。这里与插入的case2和case3是对称的。

CASE 3:$w$ is black , $w.left.color$ is red,and $w.right.color$ is black

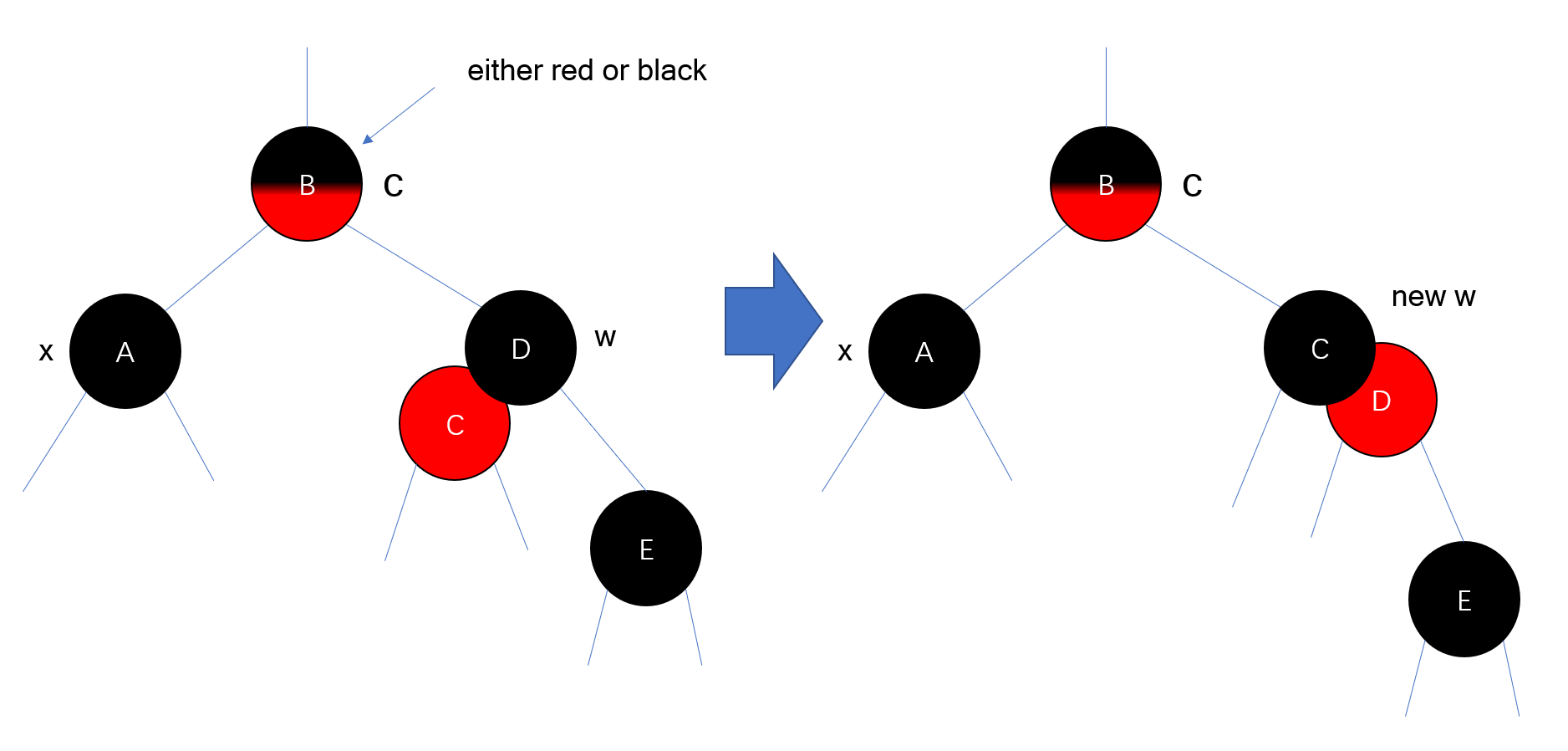
CASE3是CASE4的过渡态。主要是为了让红节点成为兄弟的右孩子，这个并不难，我们只需要把左孩子转换成右孩子

重染色：$w.left.color=BLACK,w.color=RED$
右旋改变链接：$RIGHT-ROTATION(w)$
重定兄弟：$w=x.p.right$

变换前后黑节点数并未变化，请自行验证

CASE 4:$w$ is black and $w.right.color$ is red

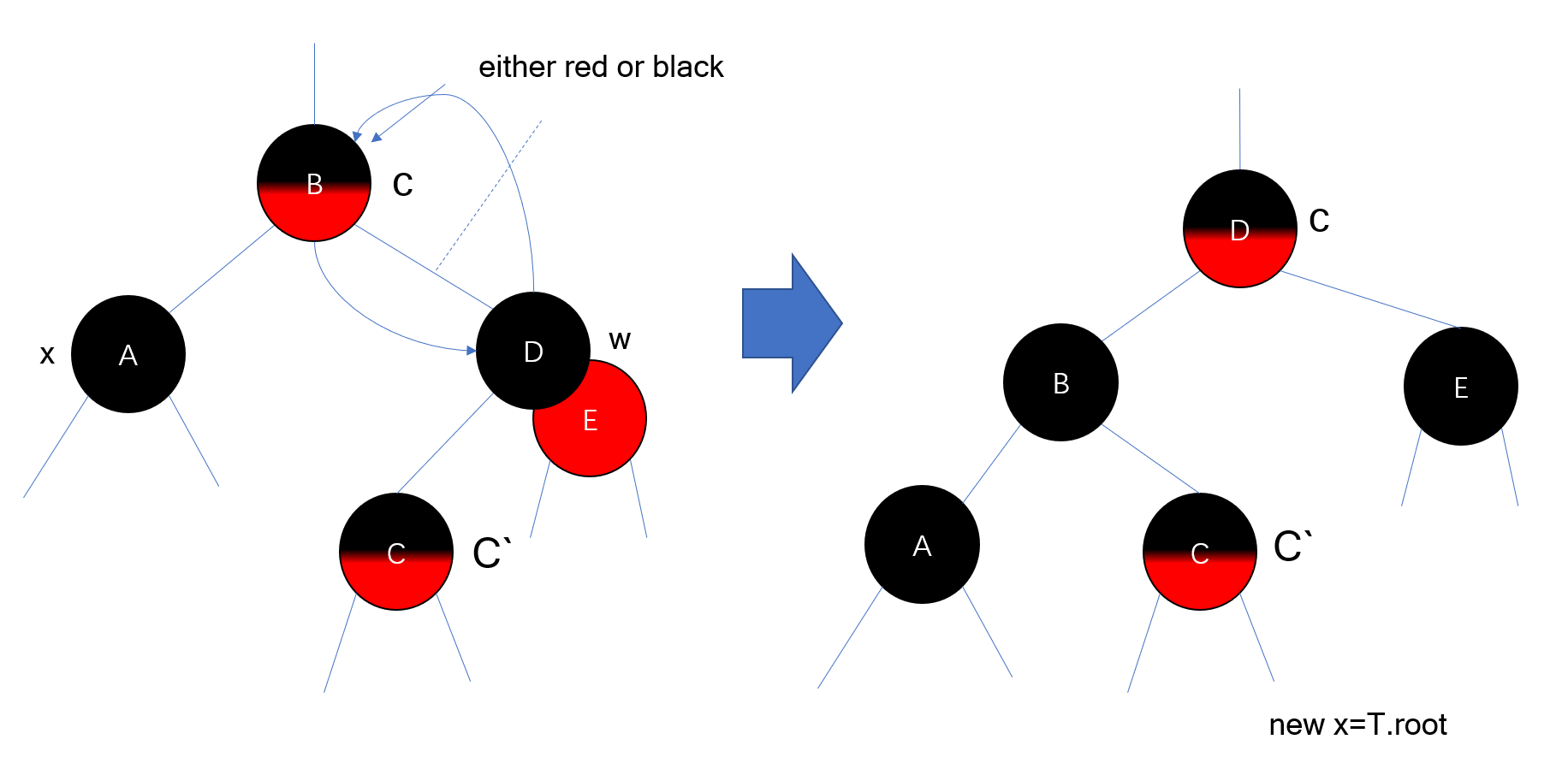
具体流程在上两张图中有，之后令$x$为树根节点退出循环便可。

接下来，伪码就不难写出：

RB-DELETE(T,z)
y ← z
y-original-color ← y.color
if z.left = T.nil
 then x ← z.right 
 	  RB-TRANSPLANT(T,z,z.right)
 elseif z.right = T.nil
  then x ← z.left
  	   RB-TRANSPLANT(T,z,z.left)
  else y ← TREE-MAXIMUM(z.right)
       y-original-color ← y.color
       x ← y.right
       if y.p = z
        then x.p = y
       else TREE-TRANSPLANT(T,y,y.right)
             y.right ← z.right
             y.right.p ← y
       TREE-TRANSPLANT(T,z,y)
       y.left ← z.left
       y.left.p ← y
       y.color ← z.color
        
if y-original-color = BLACK
 then RB-DELETE-FIXUP(T,x)
 
RB-DELETE-FIXUP(T,x)
while x ≠ T.root and x.color = BLACK
 do if x.p.left = x
 	 then w ← x.p.right
 	      if w.color = RED   									//<CASE1>
 	       then x.p.color ← RED
 	            w.color ← BLACK
 	            LEFT-ROTATION(T,x.p)
 	      if w.right.color = BLACK and w.left.color = BLACK		//<CASE2>
 	       then w.color ← RED
 	            x ← x.p
 	       else 
 	       		if w.right.color = BLACK						//<CASE3>
 	       		 then w.color ← RED
 	       		      w.left.color ← BLACK
 	            	  RIGHT-ROTATION(T,w)
 	            	  w ← x.p.right
 	             w.color ← x.p.color								//<CASE4>
 	             x.p.color ← BLACK
 	             w.right.color ← BALAK
 	             LEFT-RATATION(T,x.p)
 	             x ← T.root
    else
     <with "left" and "right" swapped>
x.color ← BLACK

时间复杂度

分析和$RB-INSERT$差不多：

首先一般的BST删除$\rightarrow O(lgn)$

$RB-DELETE-FIXUP$

设CASE $x$的时间为$T_x$

$T_1=T_3=T_4=O(1),T_2=O(lgn)$

综上，整个删除步骤时间复杂度为$O(lgn)$

总结

红黑树的性质共有4条，切记！（忘说了，也可以是5条，有的说法把根节点和叶子节点为黑分成了两条，比如CLRS上就是5条）

这4条性质也不需要你死记硬背，你只要搞懂了为什么需要这四条性质，自然记得（参考上面红黑树高度的证明）

红黑树相比一般的BST要修改插入和删除，因为要维护红黑树的性质。

插入需要考察uncle的颜色，在性质3被破坏时，grandpa是一定存在的，uncle为叶子也可（体现了作为哨兵的好处：拥有颜色）

插入除一个过渡态CASE2，实际上只有两种情形：

uncle是红（CASE1），将parents和uncle染黑，grandpa染红，从而将破坏部分上移，直到进入CASE2或CASE3或循环终止
uncle是黑，$x$，parents和grandpa在一条线上（CASE3）而不是”<”形（CASE2）

（吐槽：插入相比删除那真是弟弟）

删除需要考察sibling及其孩子的颜色，sibling一定不是叶子，因此一定有孩子（叶子节点的话算黑孩子嘛）

删除操作涉及两个过渡态，起调整作用的情况也只有两种情形，但是更为复杂，因为你破坏了3个性质，而不是插入那样只破坏一个（其实CASE2和CASE3也不一定会被破坏，而且它们都是维护性质4送的，维护起来很简单）

sibling是红，过渡到sibling是黑（CASE1），进入CASE2，CASE3，CASE4（为什么要这么做，上面写了）
sibling是黑
- 双黑（CASE2），将extra black和sibling的黑色给parents，parents作为新的$x$：
  - 若parents为红色，染黑就此打住；
  - 若parents为黑色，即双黑点，继续循环（与插入CASE 1的IDEA一样，将破坏上移）
- 左红右黑（CASE3），过渡态。将左红转化为右红（CASE4）
- 右红（左任意，CASE4）。通过旋转和重染色使得到双黑点的路径的黑节点增多从而平摊黑色（与插入CASE 3的IDEA一样，通过旋转和重染色修复被破坏部分）

所以插入和删除的IDEA是一致的，能够将破坏上移就上移，直到能修复它（当然一直上移也可以修复，只不过插入会使得黑高增1而删除会使得黑高减1但不违反性质4，为什么会出现这种情况呢？因为我们将破坏上移，一般不会到根节点，这样新的破坏位置就是子树根节点，是路径途经点，而树根节点的话，插入时，红色会染黑，而原来的红色染黑了，黑高增1；删除时，黑色吸收的extra black无法吐出来而吃的黑高减1，可以自己画图试试）

（注意以上所有情形都是相对uncle或sibling在左边的情形，实际上还有对称情形省略了）