搜索二叉树

这里不对搜索二叉树做出定义，仅讲解主要操作

DATATYPE

结点属性为$left,right,p(arents),key$，分别表示左孩子，右孩子，父（母）节点，键值

树仅保存$root$，表示整个树的根节点

$NIL$表示该位置为空（一般用空指针表示）

INSERT

我们用$y$来表示trailing pointer,$z$表示欲插入的结点，$y$跟踪$z$，指向其父节点，即$z.p$。

为了维护BST的性质，我们需要与当前根节点进行比较，找到合适的空地插入，也正因此需要$y$来告诉我空地位置在哪，以便更新其父节点

伪码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
TREE-INSERT(T,z)
x ← T.root
y ← NIL

while x ≠ NIL
 do y ← x
    if z.key<x.key
     then x ← x.left
     else 
      then x ← x.right

z.p ← y
if y=NIL
 then T.root ← z
 elseif z.key<y.key
  then y.left ← z
  else 
   then y.right ← z

和插入思路差不多，利用BST的性质进行搜索，因为二分，所以时间复杂度为$O(h)$

递归版本

1
2
3
4
5
6
7
TREE-SEARCH-RECURSION(x,k)
if(x = NIL or k = x.key)
	return x
if k<x.key
 then TREE-SEARCH-INCURSION(x.left,k)
 else 
  then TREE-SEARCH-INCURSION(x.right,k)

迭代版本

1
2
3
4
5
6
7
8
TREE-SEARCH-INTERATIVE(x,k)
while x ≠ NIL and k ≠ x.key
 do if k<x.key
 	 then x ← x.left
 	 else
 	  then x ← x.right
 	  
return x

MAXIMUM&MINIMUM

这个十分简单，直接给出伪码：

1
2
3
4
5
6
7
8
9
10
11
TREE-MAXIMUM(x)
if x.right ≠ NIL
 then x ← x.right
 
return x

TREE-MIMIMUM(x)
if x.left ≠ NIL
 then x ← x.left
 
return x

这里顺便给出习题12.2-2的答案：写出$TREE-MAXIMUM$和$TREE-MIMIMUM$的递归版本

尾递归改成迭代十分简单，反之亦然：

1
2
3
4
5
6
7
8
9
10
11
TREE-MAXIMUM-RECURSION(x)
if x.right = NIL
 then return x
 
TREE-MAXIMUM-RECURSION(x.right)

TREE-MINIMUM-RECURSION(x)
if x.left = NIL
 then return x
 
TREE-MINIMUM-RECURSION(x.left)

SUCCESSOR

SUCCESSOR可译作“后继”，表示大于该节点的最小节点

  • 当右子树不为空时，直接用$TREE-MINIMUM(x.right)$得到右子树最小值即可

  • 当右子树为空时

这里引入一个定理：

Problem 12.2-6

Suppose a binary search tree $T$ whose keyss are distinct.Show that if the right subtree of a node $x$ in $T$ is empty and $x$ has a successor $y$,then $y$ is the lowest ancestor of $x$ whose left child is also an ansestor of $x$.

这个定理实际上就是习题12.2-6的题干,我们将证明这是正确的

祖先是指根节点到该节点的路径上的所有节点，包括该节点本身，真祖先才不包括本身

$Proof:$

因为右子树是空的，假设后继在左子树中，则根据BST性质得到：$y<x$，与$y$是$x$的后继矛盾

因此$y$一定是$x$的祖先。

假设$y$的右孩子是$x$的祖先，那么$x$出现在$y$的右子树中，意味着$x>y$，与$y$是$x$的后继矛盾

因此$y$的左孩子一定是$x$的祖先。

假设$y$不是最近的祖先，则$\exists y’ \ne y$是具有“左孩子为$x$祖先”性质的最近祖先

$x$在$y’$的左子树中，而$y’$必然在$y$的左子树中，则必然有$x < y’ <y$，$y$是$x$的后继矛盾，故不存在这样的$y’$使得$y$是$x$的后继，

i.e.$y$是$x$的最近祖先且其左孩子为其祖先 $\blacksquare$

另外，

  • 当$y.left \ne x$，那么$x$不可能在$y.left$的左子树中，否则$y.left$会成为具有”左孩子为$x$祖先”性质的最近祖先，与$y$矛盾

因此$x$必然在$z$的右子树中

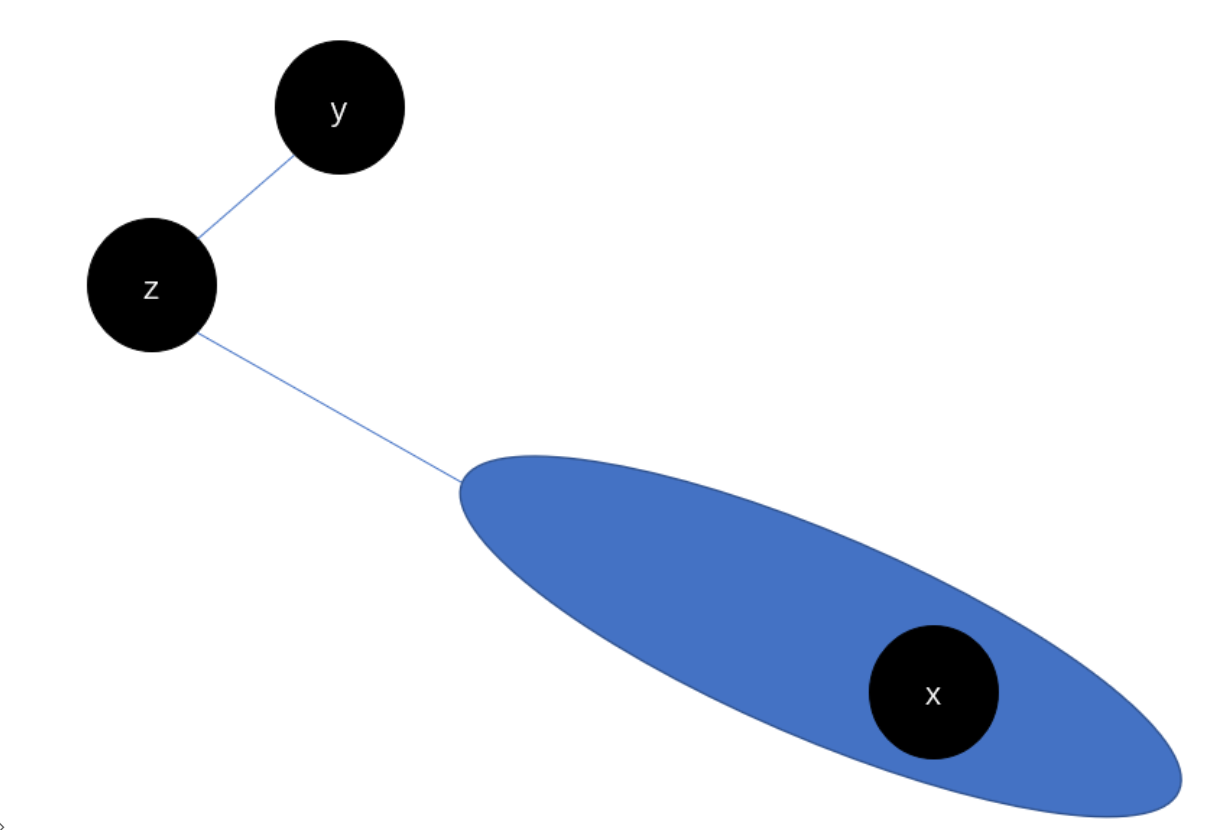
这样我们可以得到右子树为空的节点后继的树模型（蓝色椭圆表示右子树，其中允许有左孩子）：

image.png

  • 当$y.left =x$时，因为$x$可以是$x$的祖先，亦然满足条件

image.png

前继与后继是对称的，不难得知：

前继一定是最近祖先且其右孩子为其祖先

  • 还有一点，当右子树不为空时，需不需要考虑比给定结点大的祖先？不需要

用$x$表示给定节点，$z$表示祖先，假设$x$在$z$的左子树中，$y=TREE-MINIMUM(x.right)$，那么$x<y<z$，因此$y$是$x$的后继

又假设$x$在$z$的右子树中，则$z<x<y$，$y$依然是$x$的后继，因此当右子树不为空时，不需要考虑比$x$还大的祖先

根据以上信息，用伪码表示：

1
2
3
4
5
6
7
8
9
10
TREE-SUCCESSOR(x)
if x.right ≠ NIL
 then return TREE-MINIMUM(x.right)
 
y=x.p
while y ≠ NIL and y.right = x
 do x ← y
  	y ← y.p

return y

12.2-3习题是给出TREE-PREDECESSOR的伪码：

1
2
3
4
5
6
7
8
9
10
TREE-PREDECESSOR(x)
if x.left ≠ NIL
 then return TREE-MAXIMUM(x.left)

y=x.p
while y ≠ NIL and y.left = x
 do x ← y
 	y ← y.p

return y

DELETE

删除操作我们要分类讨论，分为3类

  • CASE1：没有孩子。直接删除，不需要处理链接方式
  • CASE2：有一个孩子。让该孩子顶替它即可
  • CASE3：有两个孩子。我们用该节点的后继来顶替它，并把该节点的左子树转交给后继。

PS：你可能会说直接CASE3为什么不用右孩子或左孩子直接顶替？那是因为孩子与该节点不一定很接近，e.g.右孩子比该节点大很多，左子树不为空，又需要接手原节点的左子树，可能会使树变高（而且很麻烦），而后继的左子树为空，没有这个顾虑，所以我们用最接近的后继顶替。而CASE2不需要考虑后继（前继），是因为不需要转交左子树（右子树），树并没有变高的问题

补充：

Problem 12.2-5

Show that if a node in a binary search tree has two children,then its successor has no left child and its predecessor has no right child

这是习题12.2-5的题干。

证明十分简单，由定义即可得：因为右子树所有节点大于根节点，因此后继作为最小节点必然是最左的，即无左子树

实际上，因为后继和前继对称，CASE3换成前继也可以，只不过得转交右子树。

TREE-TRANSPLANT

因为删除操作涉及顶替，我们需要准备一个顶替操作，称为$TARANSPLANT$，

设$v$为原节点，欲顶替节点为$u$，处理的树为$T$，先判断$v$是否为根节点，如果是根节点，直接更新$T.root$，否则将$v.p’s$的孩子重定向为$u$，然后根据$u$是不是$NIL$，决定是否重定向$u.p$，移植操作并不处理链接方式，链接方式由$TREE-DELETE$设置

PS：实际上，你可能会想重定向孩子可以直接$v=u$，为什么要通过$v.p$？因$v=u$使得顶替节点占据了原节点位置，这样在$TREE-DELETE$中会删除$u$，而不是$v$，因此通过$v.p$重定向，这样不会弄混节点的绝对位置

1
2
3
4
5
6
7
8
9
TREE-TRANSPLANT(T,v,u)
if v.p = NIL
 then T.root ← u
 elseif v.p.right=v
  then v.p.right ← u
  else v.p.left ← u

if u ≠ NIL
 then u.p ← v.p

CASE 1，2：

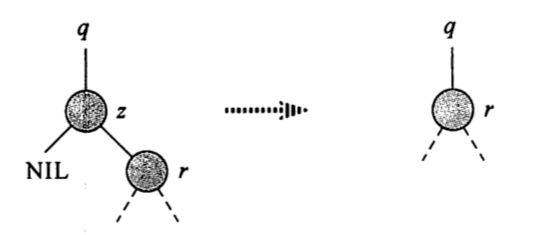
image.png

image.png

实际上，CASE 1并入到了CASE 2中，当左（右）子树为NIL时直接将NIL顶替原节点，再删除即可

CASE 3

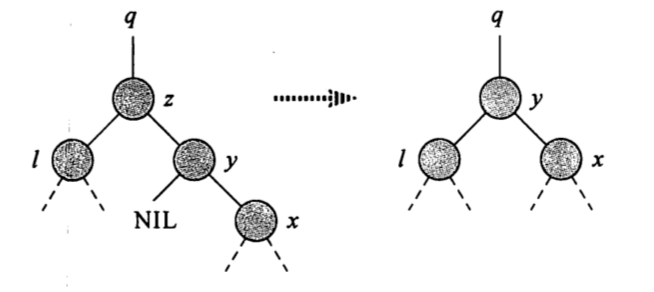
image.png

当右孩子正好是后继时，我们可以直接将$y$顶替上去，再讲$l(z.left)$重定向即可

19~BZ20_JF7~VTLYU__NW_B.png
如果右孩子不是后继，则后继在右子树的最左，我可以把$x(y.right)$转交给$y.p$，而$y$与$r(z.right)$重构链接关系，实际上$z$和$y$的链接属性并不重要，因为$TRANSPLANT$并不关注链接属性，然后接手$l(z.left)$即可

根据这些信息，我们可以写出如下伪码：

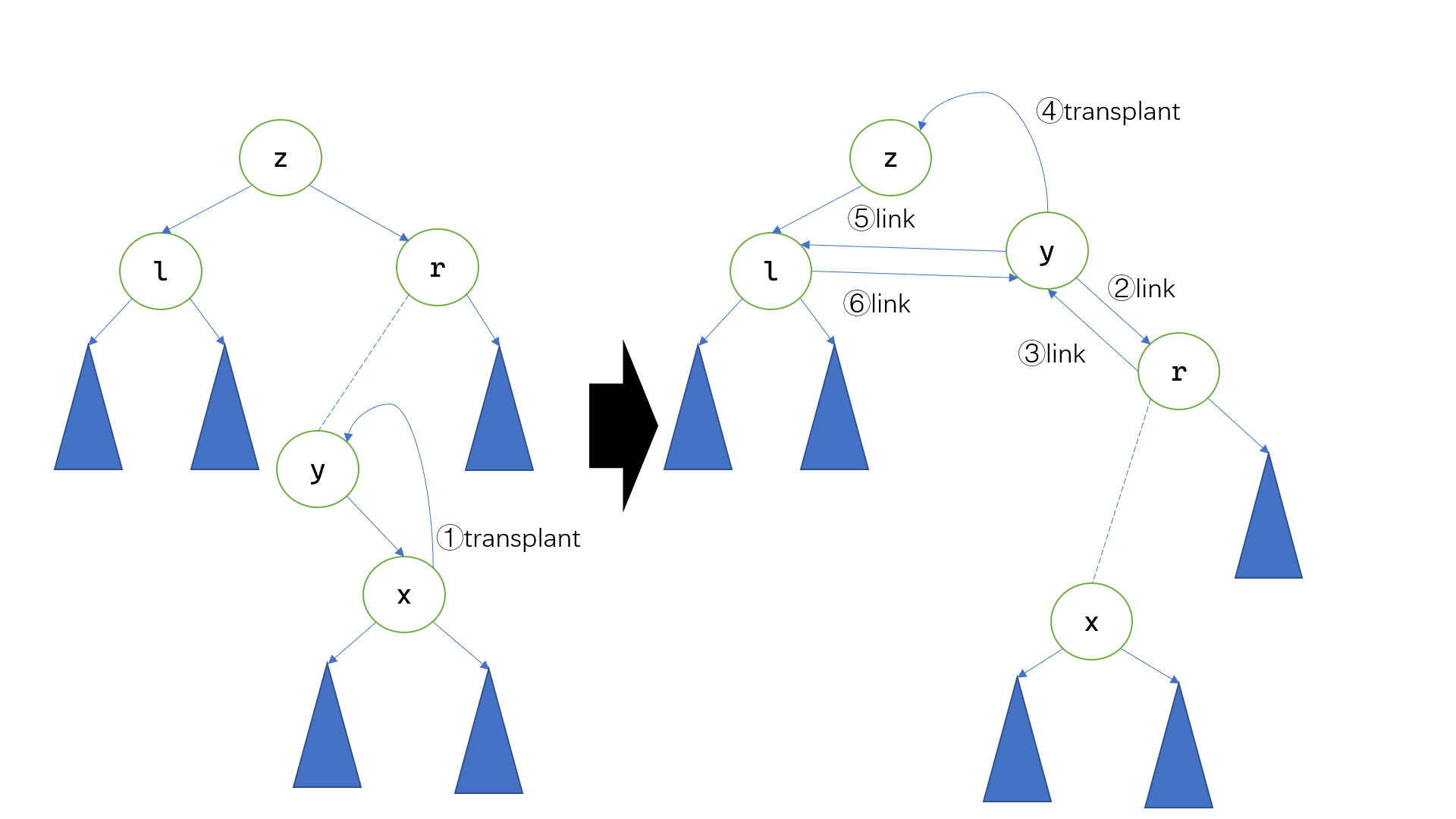
1
2
3
4
5
6
7
8
9
10
11
12
13
14
TREE-DELETE(T,z)
if z.right = NIL
 then TREE-TRANSPLANT(T,z,z.left)
 elseif z.left = NIL
  then TREE-TRANSPLANT(T,z,z.right)
  else
   then y ← TREE-MINIMUM(z.right)
    	if y ≠ z.right
    	 then TREE-TRANSPLANT(T,y,y.right)
    	 	  y.right ← z.right
    	 	  y.right.p ← y
    	TRANSPLANT(T,z,y)
    	y.left ← z.left
    	y.left.p ← y

时间复杂度

以上所有操作除$TREE-TRANSPLANT$为$O(1)$，其他的均为$O(h)$

如果我是以有序序列构造该二叉树的话，那么会成为左（右）斜树，即链状，那么时间复杂度就为$O(n)$。

因此一般的BST不能保证高度保证在一定范围，使得效率得不到保证。

下一次我们通过红黑树的构建，可以得到一个$O(lgn)$的BST

C++ implementation

别问我为什么不用class组织，我就是想用最土味的C写一下（好吧模板是C++的，不过只是最基础的运用罢了）

其实还可以提供clone进行拷贝（至于移动就只要移动$T.root$就行了），makeEmpty清空树（析构的辅助函数）等其他操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
#define NIL nullptr
template<typename T>
struct BNode{
    T key;
    BNode* left=NIL;
    BNode* right=NIL;
    BNode* p=NIL;
};

template<typename T>
struct BinarySearchTree{
    BNode<T>* root=NIL;
};

template<typename T>
void treeInsert(BinarySearchTree<T> & tree,T const& item){
    BNode<T>* y=NIL;
    auto x=tree.root;
    auto z=new BNode<T>{item};
    while(x!=NIL){
        y=x;
        if(item<x->key) x=x->left;
        else x=x->right;
    }
    z->p=y;
    if(y==NIL) tree.root=z;
    else if(item<y->key) y->left=z;
    else y->right=z;
}

template<typename T>
void inorderWalk(BinarySearchTree<T> const& tree){
    inorderWalk_AUX(tree.root);
}

template<typename T>
void inorderWalk_AUX(BNode<T> const* root){
    if(root!=NIL){
        inorderWalk_AUX(root->left);
        std::cout<<root->key<<" ";
        inorderWalk_AUX(root->right);
    }
}

template<typename T>
BNode<T> const* treeSearch(BinarySearchTree<T> const& tree,T const& item){
    return treeSearch_Iterative(tree.root,item);
}

template<typename T>
auto treeSearch_Recursion(BNode<T> const* root,T const& item){
    if(root!=NIL && root->key!=item){
        if(item<root->key)
            treeSearch_Recursion(root->left,item);
        else treeSearch_Recursion(root->right,item);
    }else return root;
}

template<typename T>
auto treeSearch_Iterative(BNode<T> const* root,T const& item){
    while(root!=NIL && root->key!=item){
        if(item<root->key)
            root=root->left;
        else root=root->right;
    }
    return root;
}

template<typename T>
auto treeMaximum(BinarySearchTree<T> const& tree){
    return treeMaximum_AUX(tree.root);
}
template<typename T>
auto treeMaximum_AUX(BNode<T> const* root){
    while(root->right!=NIL){
        root=root->right;
    }
    return root;
}

template<typename T>
auto treeMinimum(BinarySearchTree<T> const& tree){
    return treeMinimum_AUX(tree.root);
}

template<typename T>
auto treeMinimum_AUX(BNode<T> const* root){
    while(root->left!=NIL){
        root=root->left;
    }
    return root;
}

template<typename T>
BNode<T> const* treeSuccessor(BNode<T> const* root){
    if(root->right!=NIL)
        return treeMinimum_AUX(root->right);

    auto y=root->p;
    while(y!=NIL && root==y->right){
        root=y;
        y=y->p;
    }
    return y;
}

template<typename T>
BNode<T> const* treePredecessor(BNode<T> const* root){
    if(root->left!=NIL)
        return treeMaximum_AUX(root->left);

    auto y=root->p;
    while(y!=NIL && y->left == root){
        root=y;
        y=y->p;
    }

    return y;
}
template<typename T>
void treeTransplant(BinarySearchTree<T> & tree,BNode<T> *oldSub,BNode<T> *newSub){
    if(oldSub->p==NIL)
        tree.root=newSub;
    else{
        if(oldSub==oldSub->p->right)
            oldSub->p->right=newSub;
        else oldSub->p->left=newSub;
    }
     if(newSub!=NIL)
            newSub->p=oldSub->p;
}

template<typename T>
void treeDelete(BinarySearchTree<T> & tree,T const& item){
    auto z=const_cast<BNode<T>*>(treeSearch(tree,item));
    if(z==NIL)
        return ;

    if(z->left==NIL)
        treeTransplant(tree,z,z->right);
    else if(z->right==NIL)
        treeTransplant(tree,z,z->left);
    else{
        auto y=const_cast<BNode<T>*>(treeMinimum_AUX(z->right));
        if(y->p!=z){
            treeTransplant(tree,y,y->right);
            y->right=z->right;
            y->right->p=y;
        }
        treeTransplant(tree,z,y);
        y->left=z->left;
        y->left->p=y;
    }
    delete z;
}