Rod Cutting
钢条切割问题
Problem:
Given a rod of length n inches and a table of prices $p_i$ for i=1,2,…,n,determine the maximum revenue $r_n$ obtainable by cutting up rod and selling the prices.Note that if the price $p_i$ for a rod of length n is large enough,an optimal solution may requires no cutting at all
长度与价格的关系表如下:
| Length i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Price $p_i$ | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
按照动态规划的两个特征,先找到该问题是否具有最优子结构(optimal substructure)性质:
先切成两段,分成两个相异的子问题,这样就会产生许多两段切割方案,然后在这些方案中取最大收益即可
原问题的最优解包含相关子问题的最优解,因此该问题具有最优子结构的性质
不过这样有两个相关子问题,因此我们考虑先切下一段长度为i的钢条(i∈[1,n]),然后只有右边剩余部分可以继续分割,这样我们就得到了所有的“先切一段”方案(当i=n时,为不切方案,不过视作“切了”,$r_0=0$),取其最大值即可,那么很容易得到如下状态转移方程:
(这里有个思维怪圈,你可能会问第一个公式怎么转换地第二个公式。两个公式的思维出发点不同但等价,第二个公式的思维是“先切一段”,因为你不论如何都会要切一段(不切视作特殊情况),左边随便切,自然不做处理,加上右边最优切割方案,加以比较即可)
伪码如下:
1 | CUT-ROD(p,n) |
翻译成C++为:
1 | int rodCut(vector<int> & p,unsigned n){ |
但是这个算法并不能称得上良好,因为它的时间复杂度为$O(2^n)$:
因为调用rodCut需要$O(1)$,加上调用子问题的开销可以得到以下递推公式:
下面通过数学归纳法证明$T(n)=2^n$:
1.当n=1时,$T(n)=T(1)=1+T(0)=2^1$,命题成立
2.假设当n=m时,$T(n)=2^m$成立
3.当n=m+1时,$T(m+1)=1+\sum ^{m}_{j=0}T(j)=1+2^0+2^1+…+2^m=2^{m+1}$,命题得证 $\blacksquare$
还有一种思路就是画出递归树(recursion tree):
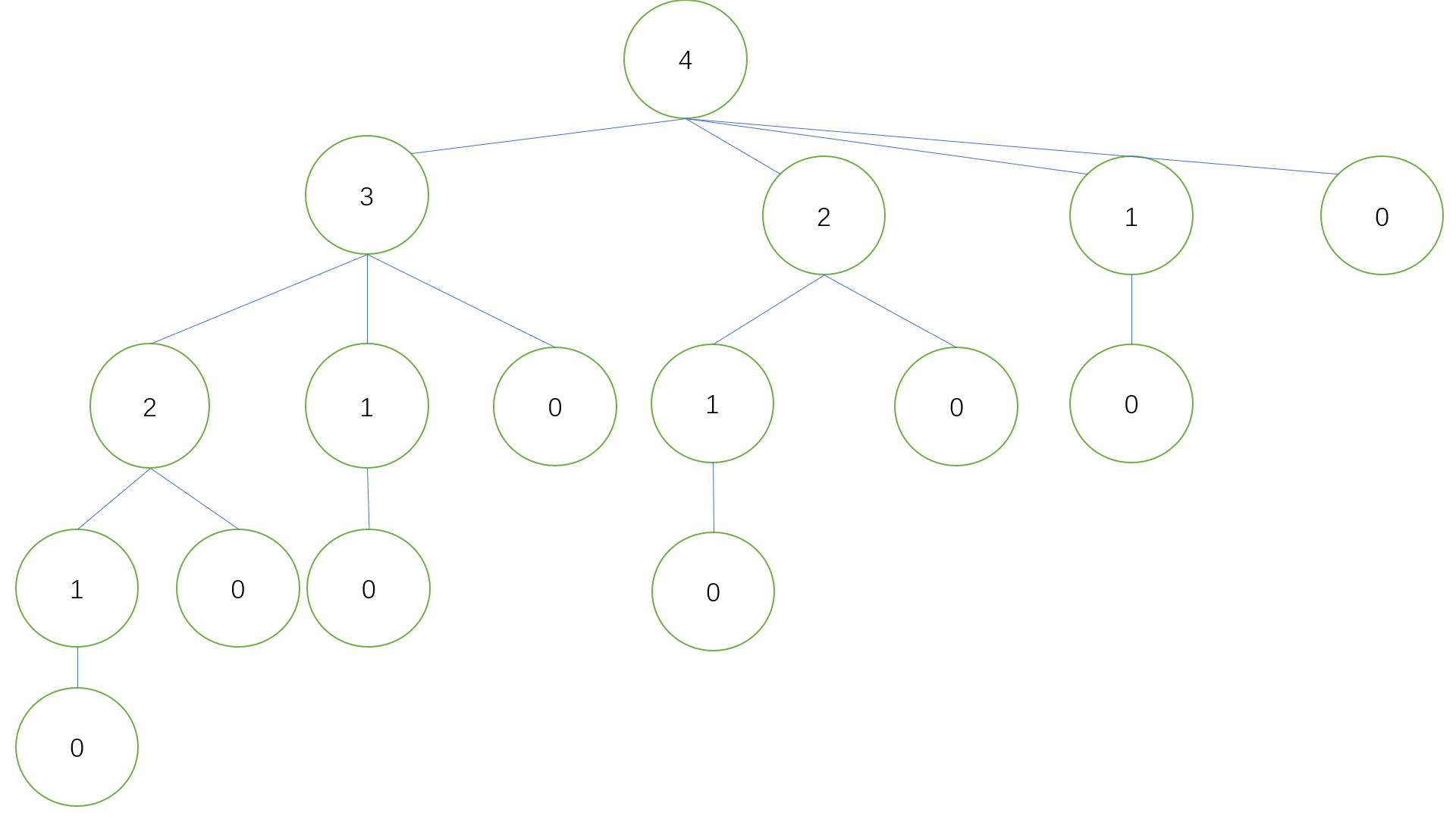
除了最上面这个根节点,其他根节点为子问题,那么总结点数与时间复杂度同阶
通过乘法原理,将切与不切看做bit,所有子问题组成bit vector,假设长度为m,那么总数目就是$2^m$,即总结点数
还有一种想法就是用牛顿二项式定理,不再赘述
由递归树可以看出该问题具备动态规划适用的第二个特征:重叠子问题(overlapping subproblem),动态规划实际优化的就是将重叠的子问题消去,只执行一次。
优化方法
top-down with memoization
上面其实用的就是自定而下的方法,这里我们通过维护一个数组来保存已经求解的结果,以便查表避免重复的执行,从而优化算法
1 | CUT-ROD(p,n) |
因为每个不同子问题只需要执行一次,共有n个不同子问题,而每个子问题都包含一个for循环,循环n次,故
$T(n)=0+1+2 +…+n =\frac {n(n+1)}{2} $~$O(n^2)$
还有一种方法,这种方法更为简单,可以说是血统最为纯正的DP
bottom-up
我们可以通过自底向上的方法优化。
子问题之间通过一个“size”进行排序,先解决”更小“的子问题,最后再来解决一个原问题,这样在解决该问题前就已经具备了解决该问题所需要的的所有先决条件。
这样我们自然不会重复计算原来的子问题,只是直接访问已解决问题的结果再来解决原问题罢了
我们用一个数组保存已解决问题的结果,以便查表
1 | BOTTOM_UP_CUT_ROD(p,n) |
这样时间复杂度取决于嵌套for循环的次数:
$T(n)=1+2+..+n= \frac {n(n+1)}{2}$~$O(n^2)$
这个方法没有用到递归而是单纯的循环,因此不需要压栈
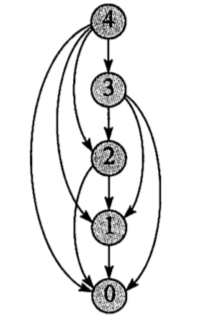
这样的图我们称之为子问题图(subproblems graph),我们注意到外层循环其实就是顶点数,而内层循环是边数。
带备忘的自顶向下法类似于DFS,而自底向上法类似于逆序拓扑排序
动态规划问题具有两个性质:
- 最优子结构:钢条切成两段,所有两段的最优切割方案中选其最大收益者即为原问题最优切割方案
- 重叠子问题:递归树有多余的“枝叶”,可以通过“修剪”得到优化
优化方案:
- 带备忘的自顶向下法:通过维护一个备忘录来达到记忆的功能避免多余的计算
- 自底向上法:从更小的子问题开始解决,待解决原问题时,已具备所有子问题最优解






