二叉堆

支持合并有左式堆和二项队列，我们实现二叉堆用最基本的数组就行了。

关键操作

insert

Example

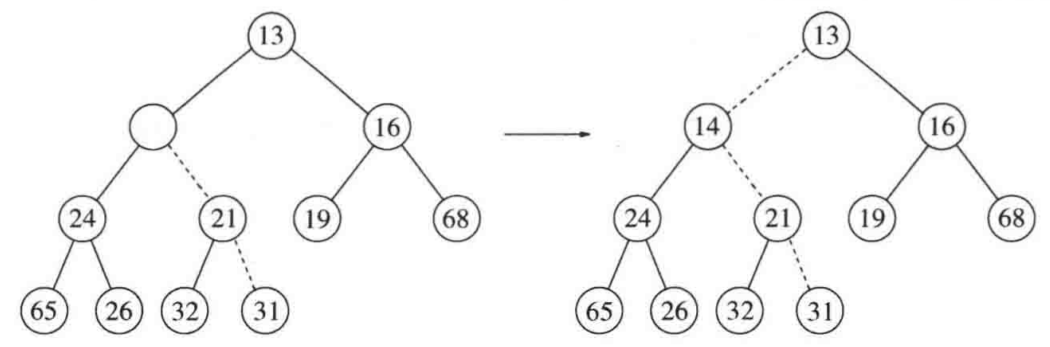
插入14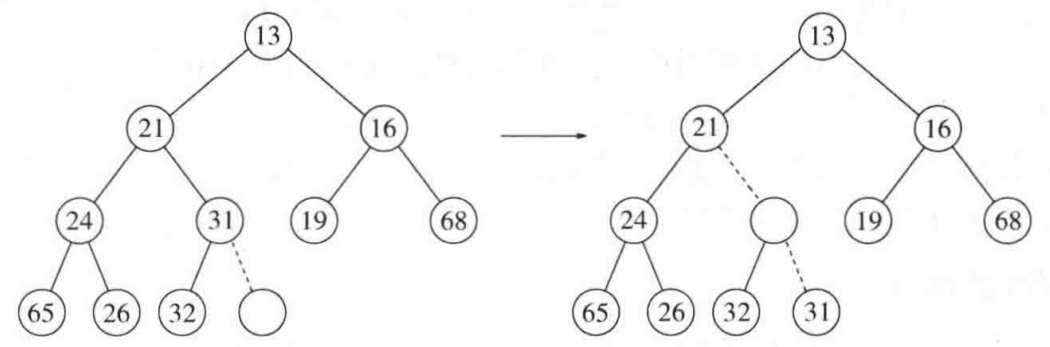

Code

template<typename T>
    void BinaryHeap<T>::insert(const T& x)
    {
        if(currentSize+1==array.size())
            array.resize(2*array.size());   //扩容

        /*
         * 上滤操作（percolate up）：与下滤操作类似，但是不是调整根结点，而是child。
         * hole是新增位置的child，其parent是最后一个父结点，通过父结点不断往上爬直到
         * 欲插入值不小于父结点停止。
         * 最后用储存插入值的哨兵填上hole。
         */
        int hole=++currentSize;
        T copy=x;

        array[0]=std::move(copy);
        for(;x<array[hole/2];hole/=2)
            array[hole]=std::move(array[hole/2]);//x<parent，hole percolate up
        array[hole]=std::move(array[0]);
    }

算法复杂度

如果insert采用一般的swap上滤，则需要3次赋值，设上滤层数为d，那么总共就需要3d次赋值，而这里的方法只需要d+1次赋值（开始哨兵不算）。
最坏情况上滤层数为[logN]，因此时间复杂度为O(logn)（平均为O(1))

deleteMin

Example

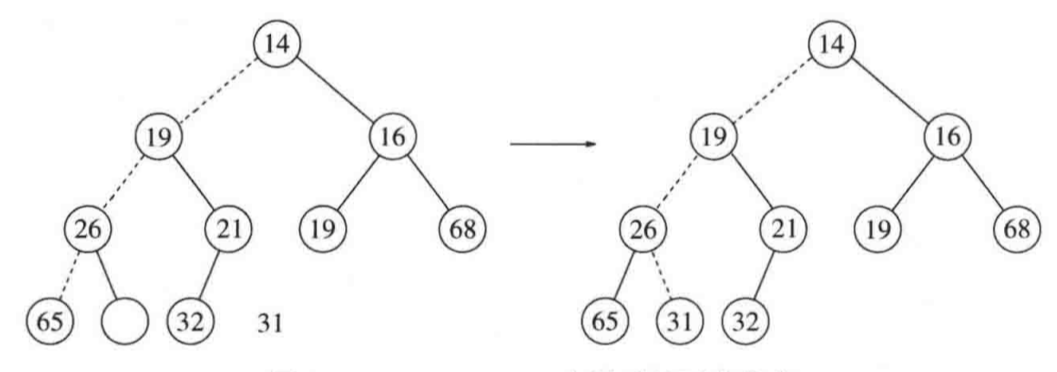
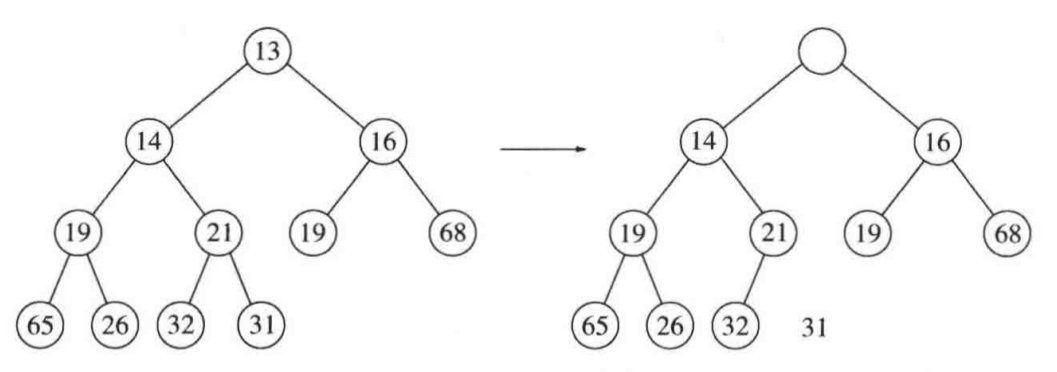
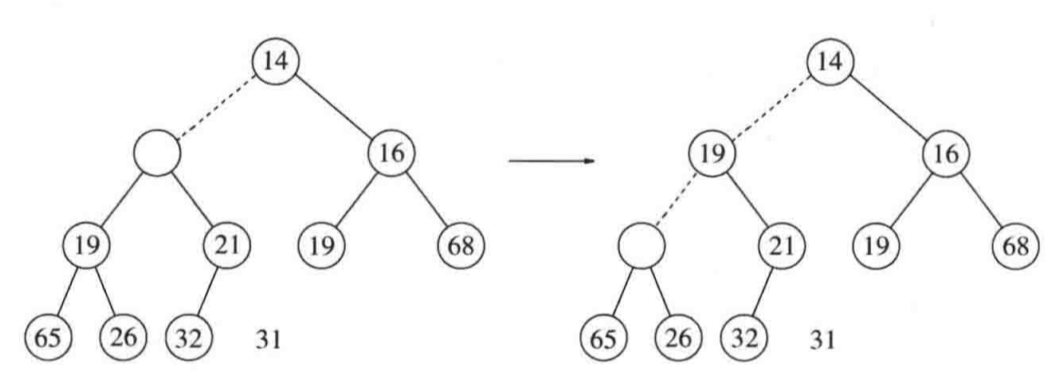
Code

void BinaryHeap<T>::deleteMin() {
        if(isEmpty())
            throw UnderflowException{};

        array[1]=std::move(array[currentSize--]);
        percolateDown(1);
    }

把最后一个叶子结点调至根结点，此时根结点失衡，于是percolateDown调整平衡维持堆序性质。

    /*
     * 下滤操作：调整失衡点（不满足堆序性质），以失衡点为根结点，在子树中找到满足堆序的位置。
     * 方式：通过child挖hole，如果最小child<失衡点，那么最小child成为失衡点的parent，原来位置成为hole，
     * 如此反复，得到一个“下滤”的形态。如果到达leaf层或已经满足堆序（到达leaf层自然满足），即可终止循环。
     * 最后用储存原来失衡点的局部变量来填上hole。
     */
template<typename T>
    void BinaryHeap<T>::percolateDown(int hole) {
        int child;
        T tmp=std::move(array[hole]);

        for(;hole*2<=currentSize;hole=child)
        {
            child=hole*2;
            if(child!=currentSize&&array[child+1]<array[child])
                ++child;    //找到最小child
            if(array[child]<tmp)
                array[hole]=std::move(array[child]);
            else
                break;  //如果array[child]>=tmp,此时已满足minheap的性质
        }
        array[hole]=std::move(tmp);
    }

算法复杂度

最坏同上滤操作，为O(logn)。

buildHeap

方案一：
通过向空堆insert来建堆，共N个insert，因此最坏时间复杂度为O(nlogn),平均为O(N)。
方案二：

/*建堆操作：从最后一个根结点开始建堆，因为每个根结点都是不平衡状态（假设）*/
void BinaryHeap<T>::buildHeap(){
        for(int i=currentSize/2;i>0;i--)
            percolateDown(i);
    }