二项队列(Binomial Queues)

名字由来

首先我们来认识一下二项队列是个什么东西，二项队列不是一颗满足堆序性质的树，而是由这些树组成的森林(forest)。

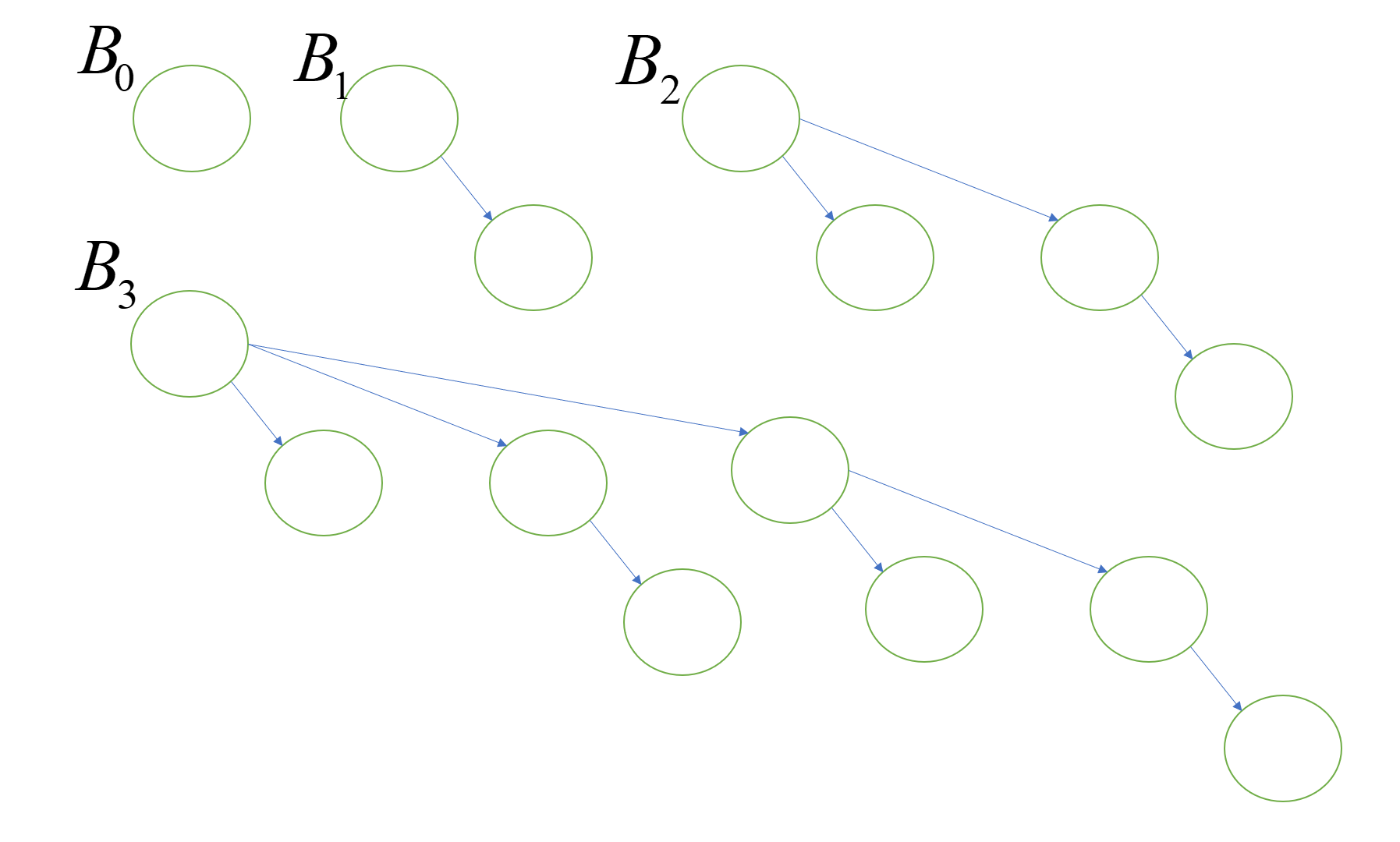
B0 B1 B2 B3

如上图所示，这是由B0、B1、B2、B3组成的二项队列，其中每一颗树都称为二项树(binomial tree)。我们将其表示为Bk。k表示二项树高度，Bk实际上是由B（k-1）接在另一个B（k-1）的根上（merge的基础）。在每个高度都只有惟一一个二项树，因此二项队列可以表示为任意大小。
二项队列为什么会如此命名，是因为二项树的性质。

性质一来源于定义，而性质二和性质三都可以通过数学归纳法得出，性质二比较显然，这里稍微证明一下性质三：

性质四也很好理解，我这里举一个例子吧，假设二项队列大小为27，27=1+2+8+16，因此可以是由B0，B1，B3，B4组成的，那么27的二进制表示就是11011，自己算算确实如此，因此我们可以根据总结点数来得出二项队列是由哪些二项树组成的。性质四实质就是十进制转二进制。

算法分析

补充一点在上面，从这点也可以看出寻找最小元素的算法分析度为O(logn)。
我们还是来重点讲一下合并操作吧。

merge

合并操作我们假设有H1和H2，如下图所示

这里先提一下rank（阶）的意思，

rank=No. of children=height of tree

我们会以H1作为新堆，合并操作结束后H2置为空，合并就是看两个二项队列中有没有同阶的，有同阶的则进行合并，没有同阶的则保留到新H1中，因此合并结果为：

从这里也可以看出我们需要提供一个同阶二项树的算法，这个在后面有所体现。

时间复杂度

合并两个同阶二项树的操作仅需常数时间，而二项树最多有O(logn)个，所以最坏情况为O(logn)。
我们再来看下插入，插入是合并的一种情形，即单结点树与二项树合并，那么最坏时间复杂度为O(logn)。最好情况呢？当二项队列为偶数时，B0是空的，此时插入就是O(1)，但是实际上我们很难遇到最坏情况，我们这里采用摊还分析来得到平均时间：

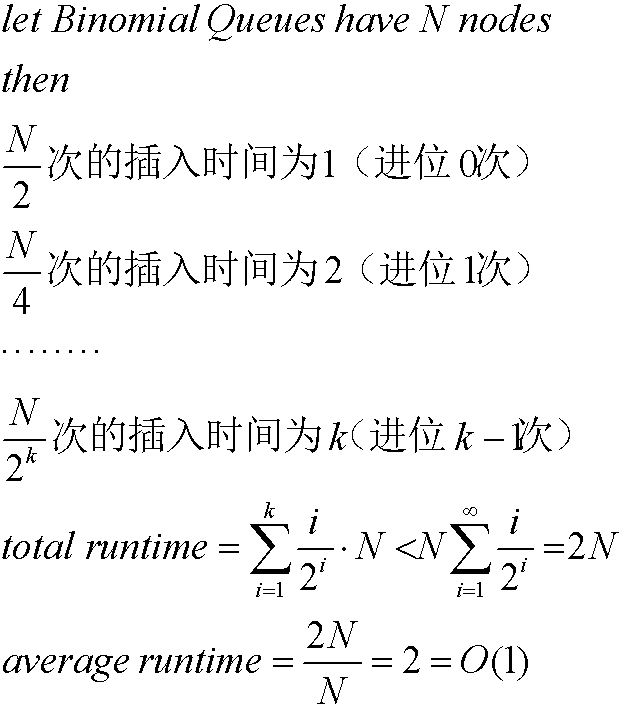
所以插入的时间复杂度取平均时间为O(1)。这就是二项队列比左式堆优越的点。

补充

deleteMin

接下来将deleteMin，我们删除掉最小根植二项树的根要如何操作？
就拿上面的H1来举例，首先我们要把最小根植和所有子树分离（假设那个点为最小根植点）

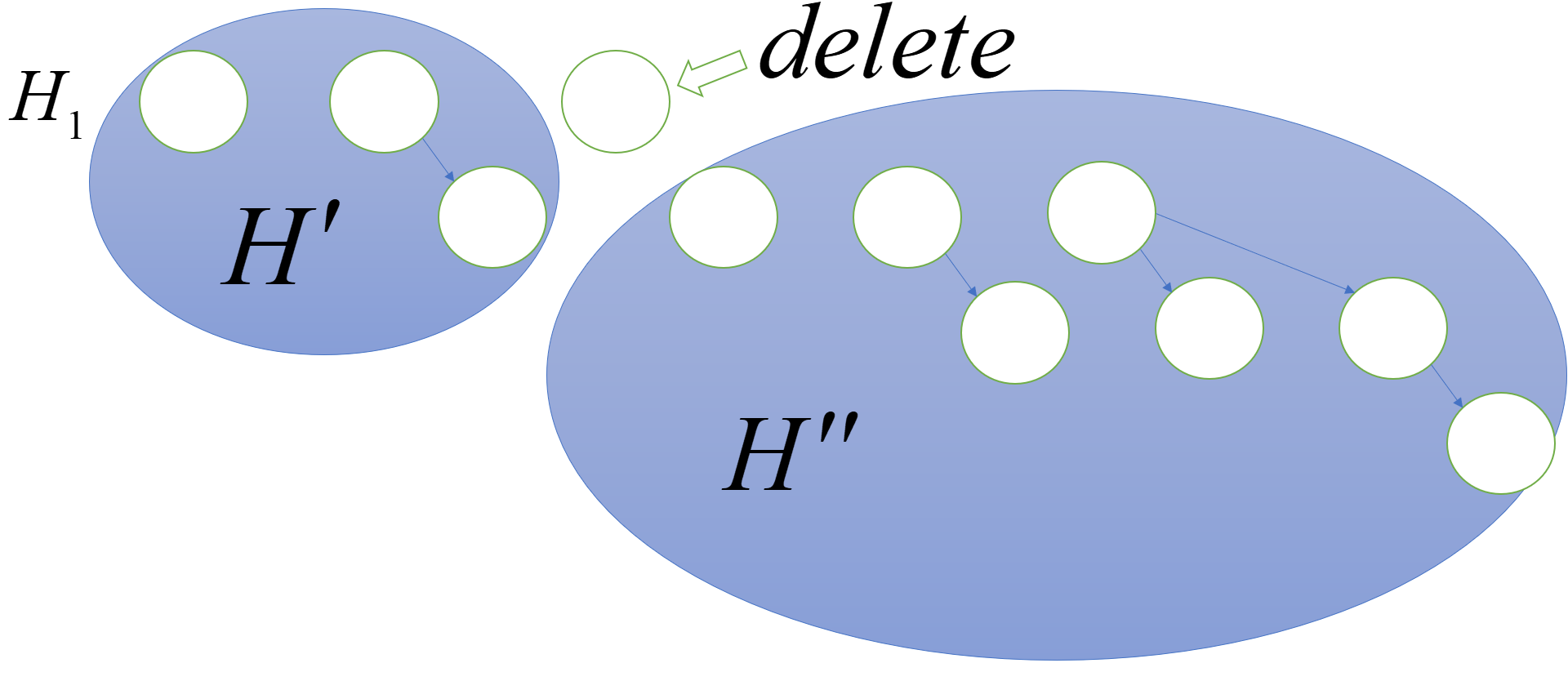
我们用H’’表示子树形成的新二项队列，而H’表示原来除最小根植树的其他二项树组成的二项队列，然后这两个二项队列进行合并，这样得到的新二项队列就是我们想要的。

时间复杂度

由上面流程可以得知分两步：找最小根植O(logn)和合并O(logn)，加起来还是O(logn)。

实现（implement）

1
2
3
4
5
struct BinomialNode{
    DataType element;
    BinomialNode* leftchild;
    BinomialNode* nextSibling;
}

用的是兄弟-儿子表示法。
同时我们会弄一个数组来存储每个根结点

1
vector<BinomialNode*> theTrees;

如用图表示大概就是这样：

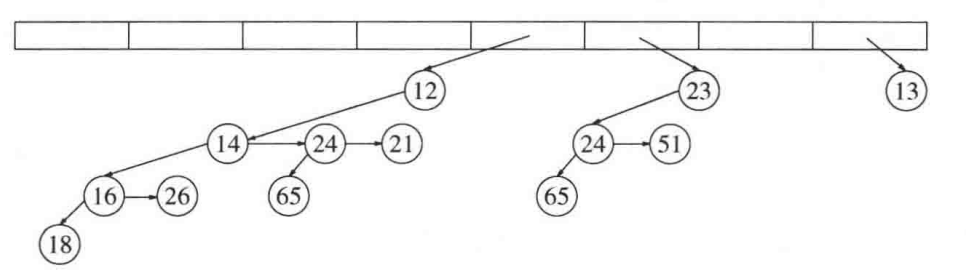
为了操作的便利，我们要求儿子按照子树的大小按顺序排列。数组的下标代表着二项树的rank。同时你会发现儿子以及兄弟都会以扩散式的递减，如图中的14是个r(2)树，而儿子和兄弟是r(1)，直至到r(0)。

我们来看下代码吧：

Source Code

capacity

1
2
3
4
int capacity()const
{
  return (1<<theTrees())-1;
}

capacity其实就是进阶的一个临界点，突破了这个临界点（currentSize>capacity()）就要重新分配根结点数组，因为我们要存储更高阶的树。

combineTrees

1
2
3
4
5
6
7
8
9
10
11
/**
 *Retuen the result of merging equal-sized t1 and t2  
 */
BinomialNode* combineTrees(BinomialNode *t1, BinomialNode *t2)
{
    if(t1->element>t2->element)
        return combineTrees(t2,t1);
    t2->nextSibling=t1->leftchild;
    t1->leftchild=t2;
    return t1;
}

这个很好理解，将小根植树儿子作为大根值的兄弟，然后大根值成为小根植的儿子（不能反过来），这样一个高一阶的新二项树就生成了。

merge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
void merge(Binomial<T> &rhs) {
    if(this==&rhs)
        return ;

    currentSize+=rhs.currentSize;
    if(currentSize>capacity())
    {
        int oldNumTrees=theTrees.size();
        int newNumTrees=std::max(theTrees.size(),rhs.theTrees.size())+1;
        theTrees.resize(newNumTrees);
        for(int i=oldNumTrees;i<newNumTrees;i++)
        {
            theTrees[i]=nullptr;
        }
    }

    BNode *carry=nullptr;

    for(int i=0,j=1;j<=currentSize;i++,j*=2)
    {
        BNode* t1=theTrees[i];
        BNode* t2=i<rhs.theTrees.size()?rhs.theTrees[i]:nullptr;


        int whichcase=t1==nullptr?0:1;
        whichcase+=t2==nullptr?0:2;
        whichcase+=carry==nullptr?0:4;

        switch(whichcase)
        {
            case 0:/*No Trees*/
            case 1:/*only this*/
                break;
            case 2:/*only rhs*/
                theTrees[i]=t2;
                rhs.theTrees[i]=nullptr;
                break;
            case 4:/*only carry*/
                theTrees[i]=carry;  //浅拷贝，转让资源管理权
                carry=nullptr;
                break;
            case 3:/*this and rhs*/
                carry=combineTrees(t1,t2);
                theTrees[i]=rhs.theTrees[i]=nullptr;
                break;
            case 5:/*this and carry*/
                carry=combineTrees(t1,carry);
                theTrees[i]=nullptr;
                break;
            case 6:/*rhs and carry*/
                carry=combineTrees(t2,carry);
                rhs.theTrees[i]=nullptr;
                break;
            case 7:/*all three*/
                theTrees[i]=carry;
                carry=combineTrees(t1,t2);
                rhs.theTrees[i]=nullptr;
                break;
        }
    }

    for(auto &root:rhs.theTrees)
        root=nullptr;
    rhs.currentSize=0;

}

这段代码我只想说真看懂了前面合并以及各标识符的意义自然就懂。
i表示的是rank，而j是i的限制条件，转换来就是i<=log（currentSize）
carry是上一步得到的树，当前case生成的carry为i+1阶，用的carry是上阶段得到的i阶。最后会以case4结束整个循环，置为nullptr（转让资源管理权）（不过不是只有最后一步才会使case4）

deleteMin

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void deleteMin(T& minItem)
{
    if(isEmpty())
        throw UnderflowException{};

    int minIndex=findMinIndex();
    minItem=theTrees[minIndex]->element;

    BNode* oldroot=theTrees[minIndex];
    BNode* deleteTrees=oldroot->leftchild;
    delete oldroot;
    theTrees[minIndex]=nullptr;

    //construct H''
    Binomial deleteQueue;
    deleteQueue.theTrees.resize(minIndex);
    deleteQueue.currentSize=(1<<minIndex)-1;
    for(int i=minIndex-1;i>=0;i--)
    {
        deleteQueue.theTrees[i]=deleteTrees;
        deleteTrees=deleteTrees->nextSibling;
        deleteQueue.theTrees[i]->nextSibling=nullptr;
    }

    //consturct H'
    currentSize-=deleteQueue.currentSize+1;

    merge(deleteQueue);
}

这个很显然的，在下面补个findMinIndex：

1
2
3
4
5
6
7
8
9
10
11
int findMinIndex()const{
    int minIndex;
    int i;

    for(i=0;theTrees[i]==nullptr;i++)
        ;//找到第一个非空根结点
    for(minIndex=i;i<theTrees.size();i++)
        if(theTrees[i]!=nullptr&&theTrees[i]->element<theTrees[minIndex]->element)
            minIndex=i;
    return minIndex;
}