左式堆（Leftist heap）

引入

二叉堆不能有效地支持合并操作，而且只使用一个数组的话，我们需要将一个数组复制到另一个数组中，时间复杂度为O(n)。因此我们通过链式来设计一个新的方便合并的堆，这就是左式堆。

性质

我们要介绍左式堆首先要介绍零路径长（null path length，简写为npl） 

 设结点X，则npl（X)=X到不具有两个儿子结点的最短路径。

所以只有一个儿子或是没有儿子的结点的零路径长为0。
左式堆的性质是：每个结点的左儿子的零路径长大于等于右儿子。因此左式堆是不平衡堆，偏向于向左增加深度，也因此便于合并，故得名——Leftist。
事实上，右路径是左式堆路径中最短的，否则，将会破坏左式堆性质。

定理

这里我们来证明一个定理：

在右路径上有r个结点的左式堆至少有2^r-1个结点

证明：

也就是说含有N个结点的左式堆，有一条最多含有[log(N+1)]个结点的右路径。
也正因此我们处理左式堆的一般思路就是将一切工作都放在右路径上进行，这样尽可能地保证了树的深度小（后面的操作有体现）。

合并操作

我们主要侧重来看一下合并是如何进行的。
先声明一下，插入是合并的一种特殊形式，看做单个点构成的左式堆与左式堆（也可能是单个点甚至为空）合并即可。
我们主要是通过递归来得到合并后的左式堆的，就像数学归纳法一样，如果一次合并成功了，那么递归得到的左式堆也应该是成功的。
下面是两个左式堆H1和H2：

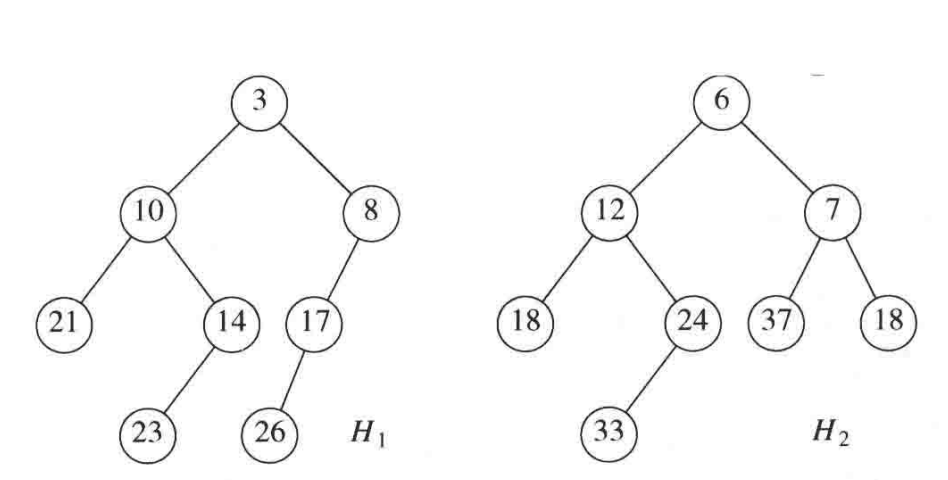
第一步是要比较两个堆的根值哪个比较大，我们递归地将较小根值的堆的右子堆与较大根值的堆合并：

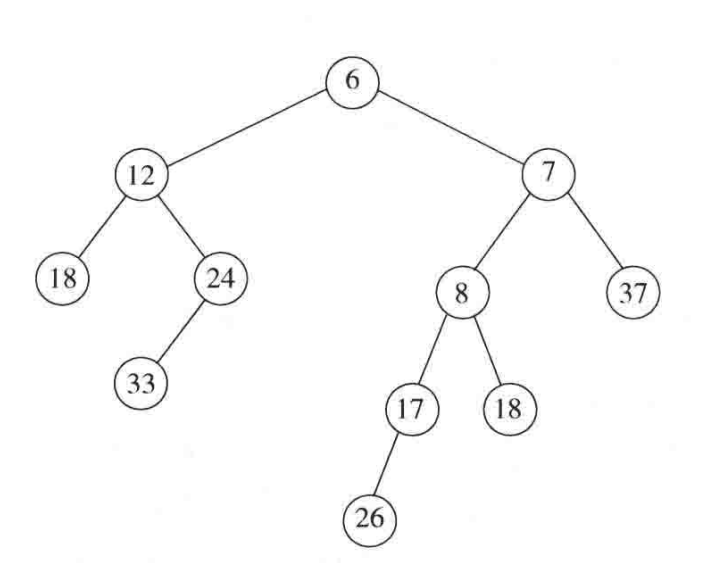
这样就得到了新的堆，这个堆会成为H1的左子堆。

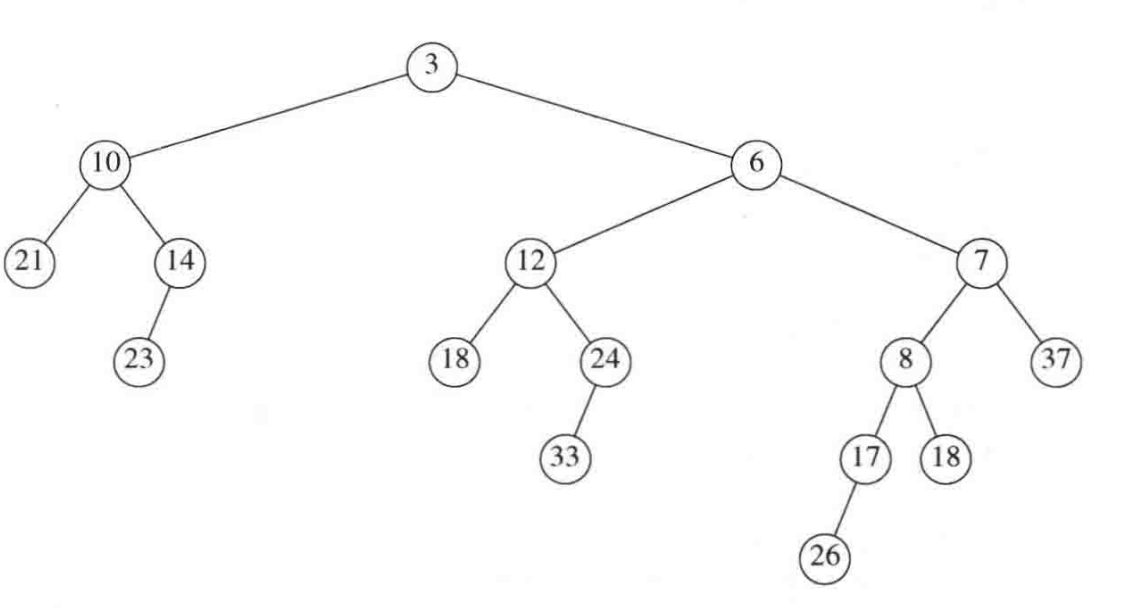
检查一下是否满足堆序性质，OK，没问题，那左式堆的性质呢？显然，左儿子的npl=1，而右儿子的npl=2，那么我们怎样维护左式堆的性质呢？很简单，只要把左右儿子对调即可。

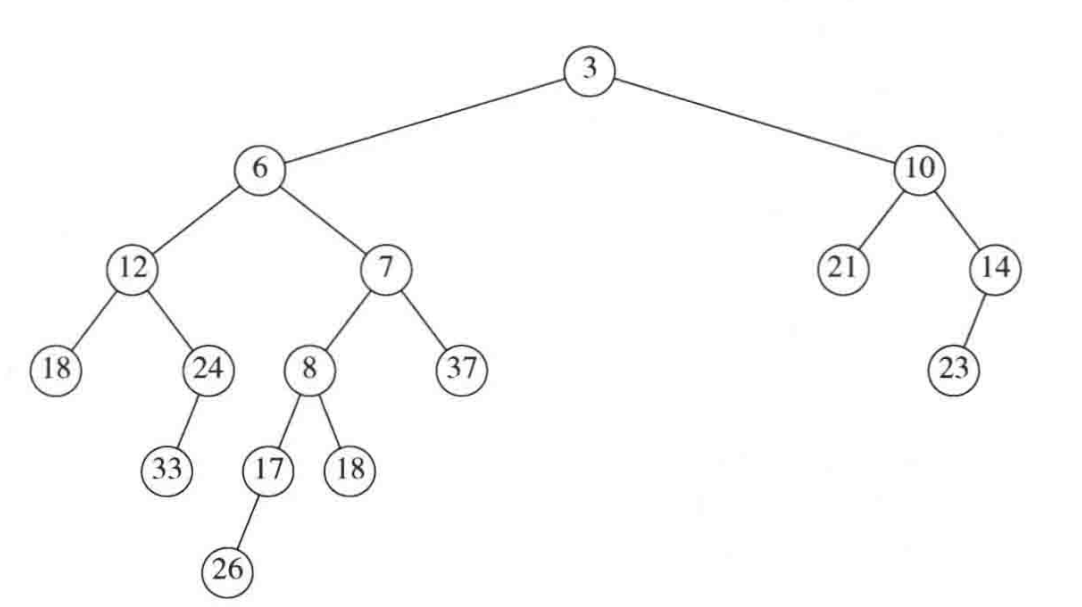
这样就得到了合并的新左式堆，新左式堆的根由原先的较小根值接手（显然）

时间复杂度

显然，通过上面的流程，我们可以得出：合并操作所用时间与右路径长度呈正比，而造访每个结点用的时间是常数时间，因此时间复杂度为O(logn)。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
template<typename Comparable>
void LeftistHeap<Comparable>::merge(LeftistHeap &rhs)
{
    if(this==&rhs)    //identity test
        return ;
    root=merge(root,rhs.root);
    rhs.root=nullptr;       //置为nullptr，将资源管理权转交给合并后的heap，避免double free
}

template<typename Comparable>
typename LeftistHeap<Comparable>::LeftistNode *
LeftistHeap<Comparable>::merge(LeftistNode* h1,LeftistNode* h2)
{
    if(h1==nullptr)
        return h2;
    if(h2==nullptr)
        return h1;
    if(h1->element<h2->element)
        return merge1(h1,h2);
    else
        return merge1(h2,h1);
}

template<typename Comparable>
typename LeftistHeap<Comparable>::LeftistNode *
LeftistHeap<Comparable>::merge1(LeftistNode *h1, LeftistNode *h2)
{
    if(h1->left==nullptr) //a single node
        h1->left=h2;
    else{
        h1->right=merge(h1->right,h2);
        if(h1->left->npl<h1->right->npl)
            swapChildren(h1);
        h1->npl=h1->right->npl+1;
    }
    return h1;
}

完整版代码请戳：LeftistHeap
可能你看到main执行之后通过中序遍历h1和h2会感到诧异，因为两个左式堆基本是平衡的，但合并后还是相对不平衡的，我们通过insert得到的两个左式堆相对平衡也是为了使合并后的新堆的深度尽可能的小，不过你要知道，左式堆合并只要能维护好其性质便好，因此一开始两个未合并的堆是不是平衡其实也不是大问题╮(╯▽╰)╭。