KMP算法

KMP由来

KMP发展自朴素模式匹配算法，但过于低效，难以处理多个0与1重复组成的字符串，因此三位大牛：D.E.knuth,J.H.Morris和V.R.Pratt发表一种新的模式匹配算法，性能远超朴素算法。
取三人名字首字母组成的算法就称为KMP算法。

朴素模式匹配算法

在学习KMP算法之前先了解下朴素匹配算法

图例分析

令文本串S=”goodgoogle”，模式串T=”google”
则步骤如下：

前三个都匹配正常，第四个匹配失败。第一位匹配失败。

显然，第二、三、四位全部匹配失败,而第五位匹配成功，从第五位开始的6个字母全匹配。

算法分析

朴素模式匹配算法就是文本串每个字符作为模式串开头来与子串匹配，
这样对文本串做一个大循环，而模式串做T的长度的小循环，直到全部匹配。

实现代码

int Violent_Match(String S,String T)
{
  int i=0,j=0;
  while(i<S.length&&j<T.length)
  {
    if(S[i]==T[j])
    {
      i++;
      j++;
    }
    else
    {
      i=i-j+1;  //i回溯
      j=0;      //j归0，模式串重新匹配
    }
  }
  if(j==T.length)
    return i-j; //返回模式串在文本串的位置
  else
    return -1;
}

算法复杂度

时间复杂度为O(mn)
其中m为文本串的长度，n为模式串的长度。

KMP算法

先说明一下朴素算法的弊端和KMP实现的关键

1.前后缀不重复的情况

如果按照朴素匹配算法的话，上面六个步骤都必须走一遍，但②③④⑤明显多余。因为b、c、d、e与已经在①中已经匹配过了，既然a与b、c、d、e都不匹配，那么就没有必要重复匹配了。

两个步骤足矣，朴素匹配显得过于赘余。

2.前后缀匹配的情况

（图中①出错了，应该是abcababca，不过也不匹配就对了）
④⑤这两步显得多余，因为前面已经前后缀匹配过了，又前后缀相同，造成了重复匹配。前缀与后缀重合的越多，赘余越多。
而且文本串不回溯，②③也可以省略。

最开始这个例子也是如此，其实在第一步就知道后面肯定失配，因为由这一步已经知道，S[1]=T[1]=’o’!=T[0],S[2]=T[2]=”o”!=T[0],T[3]=T[0]!=S[3],而这些没必要的匹配正是文本串回溯带来的弊端。

总结：

朴素匹配算法的文本串回溯在上述两种情况下显得赘余，降低了效率。因此将文本串回溯去掉，并且模式串相同前后缀省略是KMP的算法关键。

KMP算法实现关键——next数组

数学表达式

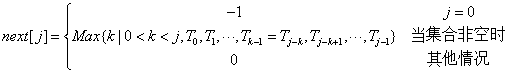
如果对于值k，已有T0 T1, …, Tk-1 = Tj-k Tj-k+1, …, Tj-1，相当于next[j] = k，即前后缀字符的最大长度。
这意味着什么呢？究其本质，next[j] = k 代表p[j] 之前的模式串子串中，有长度为k 的相同前缀和后缀。有了这个next 数组，在KMP匹配中，当模式串中j 处的字符失配时，下一步用next[j]处的字符继续跟文本串匹配，相当于模式串向右移动j - next[j] 位。
（-1用于模式串没有相同前后缀，就会回到0再匹配，若还不行则文本串右移，模式串归0重新开始新一轮的匹配）

如下图：

综上，KMP的next 数组相当于告诉我们：当模式串中的某个字符跟文本串中的某个字符匹配失配时，模式串下一步应该跳到哪个位置。如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时，下一步用next [j] 处的字符继续跟文本串i 处的字符匹配，相当于模式串向右移动 j - next[j] 位。

e.g:

j	0	1	2	3	4	5
T	a	b	c	d	e	x
next[j]	-1	0	0	0	0	0

j	0	1	2	3	4	5
T	a	b	c	a	b	x
next[j]	-1	0	0	0	1	2

j	0	1	2	3	4	5	6	7	8
T	a	b	a	b	a	a	a	b	a
next[j]	-1	0	0	1	2	3	1	1	2

j	0	1	2	3	4	5	6	7	8
T	a	a	a	a	a	a	a	a	b
next[j]	-1	0	1	2	3	4	5	6	7

KMP算法步骤：

寻找前缀后缀最长公共元素长度
求next数组
根据next数组进行匹配

实现代码

void get_next(String T,int *next)
{
  int i=0,j=-1;
  next[0]=-1;
  while(i<T.length-1)   //下标范围[0,length-1]
  {
    if(j==-1||T[i]==T[j])
    //T[i]表示后缀，T[j]表示前缀
    {
      i++;j++;
      next[i]=j;
    }
    else
    {
      j=next[j];  //j回溯到失配字符的上一个字符所对应的最长长度
    }
  }
}

int KMP_Match(String S,String T)
{
  int i=0,j=0;
  int next[T.length];
  get_next(T,next);
  while(i<S.length&&j<T.length)
  {
    if(j==-1||S[i]==T[j])
    {
      i++;
      j++;
    }
    else
    {
      j=next[j];
    }
  }
  if(j==T.length)
    return i-j;
  else
    return -1;
}

代码部分解析

j=next[j]是要去找长度更小的相同前缀后缀.
next数组存的都是失配字符的上一个字符的最长长度，也就是失配字符前面的模式串的前后缀最长长度，当T0,Tk-1,Tk与Tj-K,Tj-1,Tj匹配时，Tk与Tj失配，那么下一步就是T[next[j]]与Tj匹配。

算法复杂度

get_next函数，假设T的长度为m，其时间复杂度为O(m)，
而i的不回溯使得效率得到提升，while循环的时间复杂度为O(n),故整个算法的时间复杂度为O(m+n)

KMP优化

先来看个例子

显然②③④⑤是多余的，没必要重复匹配。
用首位next[0]去取代与它相等的字符后续next[j]的值，可以提高效率。
上面这个例子有些极端，全部都相同。
我们再来看个不极端：

前三个都匹配，到了第四个不匹配了，那么根据next[j]，向右移动j-next[j]=3-1=2个位置

向右移动2个位置依然匹配失败。但是T[next[3]]=T[1]=T[3],因此这个失败是必然的，如果将T[next[j]]=T[j]这步省略掉，KMP将会得到优化。

void get_nextval(String T,int *nextval)
{
  int i=0,j=-1;
  int nextval[0]=-1;
  while(i<T.length-1)
  {
    if(j==-1||T[i]==T[j])
    {
      i++;j++;
      if(T[i]!=T[j])  //当前字符与欲回溯字符不同
        nextval[i]=j;
      else
        nextval[i]=nextval[j];  
        //若相同，则将回溯字符的前缀位置给当前字符
    }
    else
    {
      j=nextval[j];
    }
  }
}