希尔排序

基本思想

希尔排序本质也是插入排序，又称缩小增量排序但效率打破了O(n^2)。
希尔排序是将待排序序列分成若干个小序列，并对这些小序列进行直接插入排序，待整个序列都保持“基本有序”时再对整体进行一次直接插入排序。

例子


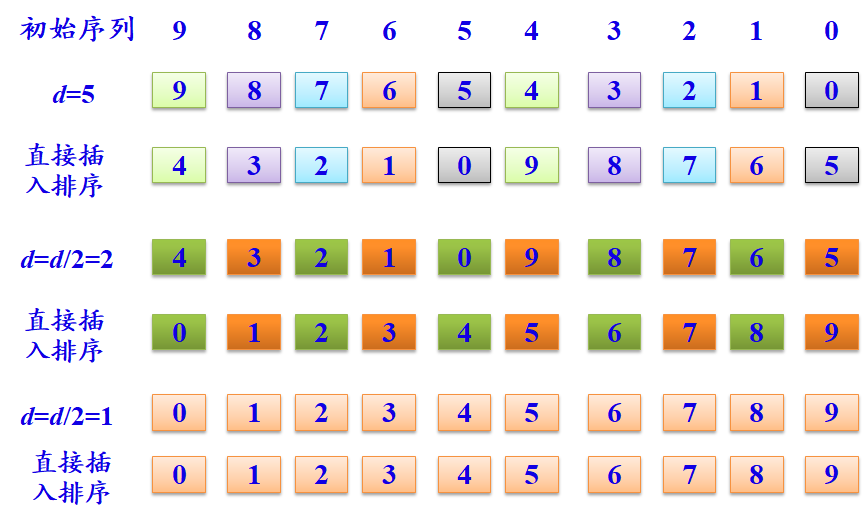
上面这个示意图正是希尔排序的实例，希尔排序通过每一小块的直接插入排序，并缩小增量，对更小的块进行直接插入排序，从而最后得到的必然是基本有序的序列，再进行一次直接插入排序，从而确定整个序列。

实现代码

采用的是除2法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void ShellSort(List &L)
{
    int i,j,temp;
    int d=L.size/2;
    while(d>0)
    {
      for(i=d;i<L.size;i++)
      {
        temp=L[i];
        for(j=i-d;j>=0&&temp<L[j];j-=d)
        {
          L[j+d]=L[j];
        }
        L[j+d]=temp;    //因为j-=d所以+d
      }
      d=d/2;
    }
}

算法复杂度

希尔排序的时间复杂度现在依然是个数学难题，不过肯定比冒泡、选择这些用空间换时间的要好，空间复杂度为O(1)。