十大排序——快速排序
快速排序
基本思想
每趟使表的第1个元素放入适当位置(归位),并且左边的元素小于这个元素,右面的元素大于这个元素,我们称这个元素为pivot,将表一分为二,对子表按递归方式继续这种划分,直至划分的子表长为0或1(递归出口)。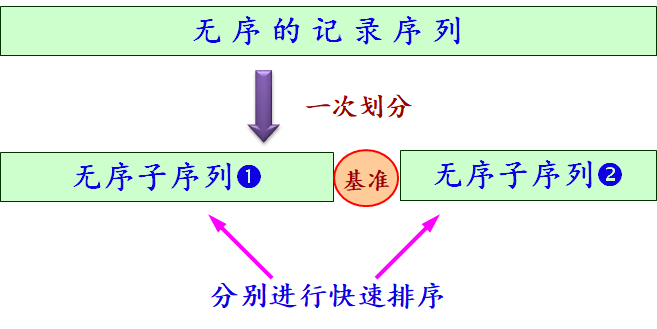
快速排序二叉递归树: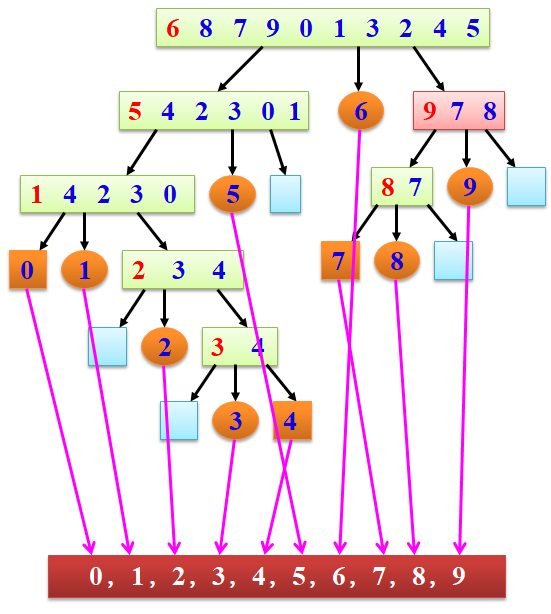
正因为是将最左边的元素提取出来当pivot,所以左边都比它小,右边都比它大,继续划分也是如此,因此这个pivot在序列中的位置就已经决定好了,其他的序列继续如此划分,直至最后分到子表长度只有1或0。由于划分是按照整体有序的方式进行的,所以最后得到的序列必然是有序的。
顺带一提,STL的sort的实现原理就是快速排序。因为相比冒泡等时间换空间的算法以及桶排序等空间换时间的算法来说,快排没有严重失衡,得到优化后更是如此,无愧于20世纪十大算法之一。
实现代码
1 | void QuickSort(List &L,int left,int right) |
算法复杂度
最好的情况:
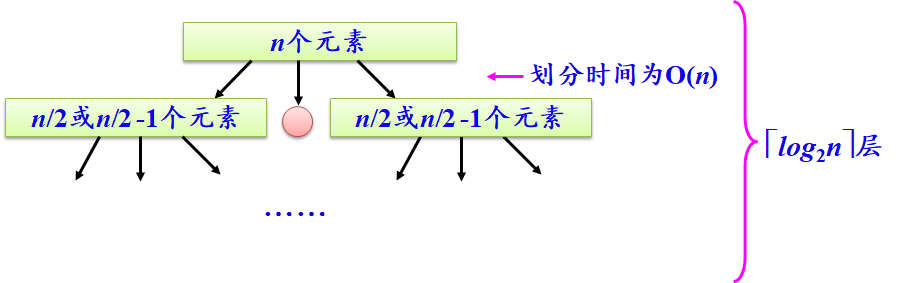
选取的pivot正好可以等分序列,每次要处理的序列长度几乎相等,经过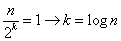 次嵌套调用,便可得到长度为1的子表,在递归树的同一级别上,没有两个调用会处理原序列的相同部分(线性),因此每个级别的调用只要O(n)次,因此整个算法的时间复杂度为O(nlogn)。
次嵌套调用,便可得到长度为1的子表,在递归树的同一级别上,没有两个调用会处理原序列的相同部分(线性),因此每个级别的调用只要O(n)次,因此整个算法的时间复杂度为O(nlogn)。
由嵌套调用次数就可知,递归树深度为logn,那么空间复杂度=O(logn)。
最坏的情况:
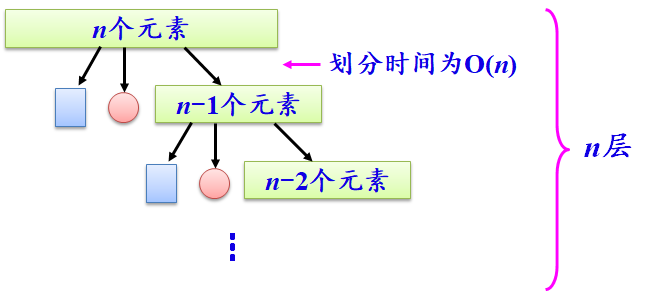
如果pivot为最大元素或最小元素,则会出现空序列和n-1的子序列,如果重复出现,则每次处理的子序列都比上次小1,这种情况下,递归树变成了n-1个嵌套调用的线性链。时间复杂度: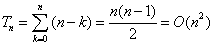
同时,递归树深度为n-1(从0开始计数,因为深度为0是非递归调用),所以空间复杂度=O(n).
平均情况:



本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Conzxy's blog!
评论






