O(logn!)=O(nlogn)

我们可以证明logn！小于nlogn而大于一个常数倍的nlogn(当n大于某一常数时）。

下面给出推导过程：
对于n>0，显然logn！<=nlogn是显然成立的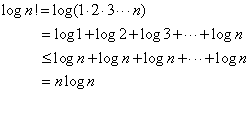

接下来，证明logn！>=Cnlogn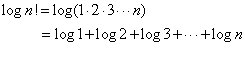

我们去掉前半部分，则可得: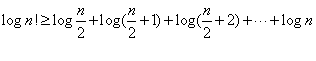

取最小项替代所有项，则：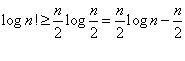

由于小于n/2logn，我们可以取其大于1/4logn: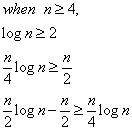


完整的步骤：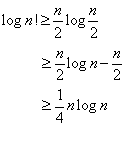

所以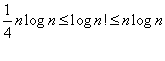

O(lgn!)=O(nlogn)证毕