归并排序

基本思路

归并排序的基本思想是：首先将a[0..n-1]看成是n个长度为1的有序表，将相邻的k（k≥2）个有序子表成对归并，得到n/k个长度为k的有序子表；然后再将这些有序子表继续归并，得到n/k2个长度为k2的有序子表，如此反复进行下去，最后得到一个长度为n的有序表。

若k=2，即归并在相邻的两个有序子表中进行的，称为二路归并排序。若k>2，即归并操作在相邻的多个有序子表中进行，则叫多路归并排序。

归并排序体现的就是分治思想。

自顶而下的排序



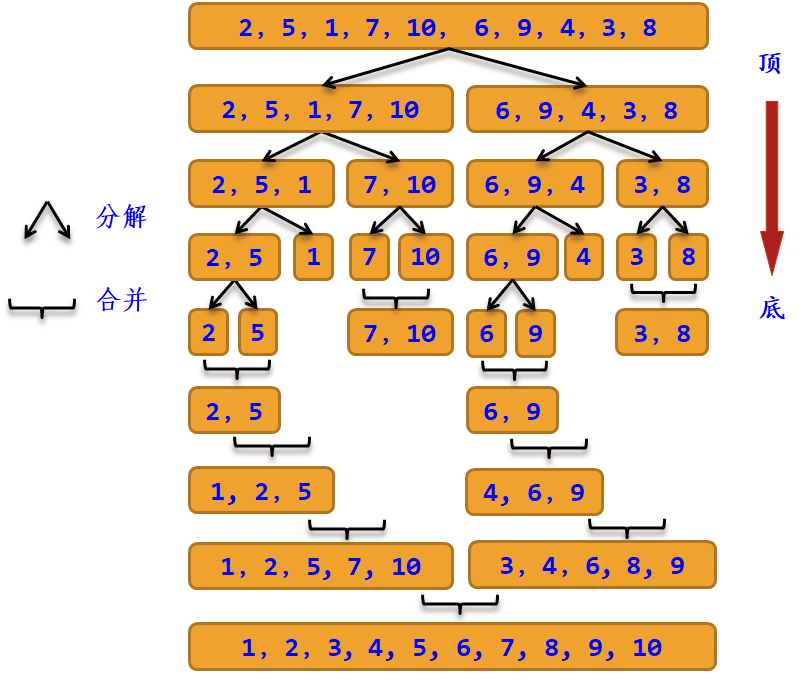
步骤：

  • 分解：将[low,high]分解成两个子表，即求mid=（low+high)/2,然后继续对[low,mid],[mid+1,high]分解，直至子表长度为1终止（因为长度为1的子表一定是有序的）
  • 归并：将排序好的两个子表[low,mid],[mid+1,high]合并

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void Merge(List &L,int low,int mid,int high)
{
    int i=low,j=mid+1;
    int k=0;
    int *temp=new int[high-low+1];
    while(i<=mid&&j<=high)
    {
      if(L[i]<=L[j])  //将第一子表放入temp
      {
        temp[k++]=L[i++];
      }
      else            //将第二子表放入temp
      {
        temp[k++]=L[j++];
      }
    }
    while(i<=mid)     //第一子表剩余的放入temp
    {
      temp[k++]=L[i++];
    }
    while(j<=high)    //第二子表剩余的放入temp
    {
      temp[k++]=L[j++];
    }
    for(k=0,i=low;i<=high;i++,k++)
    {
      L[i]=temp[k];   //拷贝temp
    }
    delete[]temp;
}

自顶而下的二路归并算法：

1
2
3
4
5
6
7
8
9
10
11
void MergeSort_top_to_bottom(List& L,int low,int high)
{
    int mid;
    if(low<high)  //子序列有两个及以上元素
    {
      mid=(low+high)/2;
      MergeSort_top_to_bottom(L,low,mid);     //对[low,mid]子序列排序
      MergeSort_top_to_bottom(L,mid+1,high);  //对[mid+1,high]子序列排序
      Merge(L,low,mid,high);    //合并两个子序列
    }
}

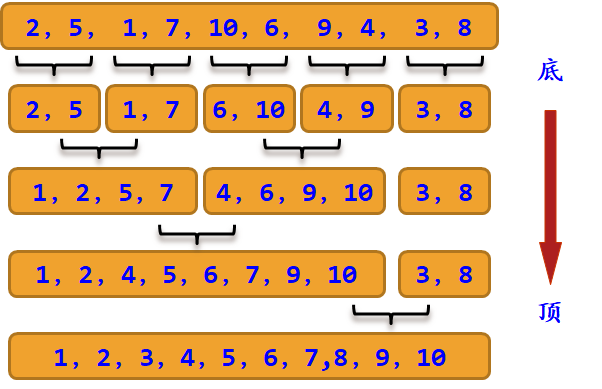
自底而上的归并排序

)

步骤：

  • 分解：将原序列分解成length长度的子序列
  • 归并：将相邻的两个子序列调用Merge合并成一个有序子序列
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void MergePass(List &L,int length,int n)  //一趟二路归并（一个length对应一趟）
    {
          int i;
          for(i=0;i+2*length-1<n;i=i+length*2)   //长度为length的两个子表归并
          {
            Merge(L,i,i+length-1,i+2*length-1);
          }
          if(i+length-1<n)        //剩余两个子表归并（后者长度小于length）
          {
            Merge(L,i,i+length-1,n-1);
          }
    }
    1
    2
    3
    4
    5
    6
    7
    void MergeSort_bottom_to_top(List &L,int n)
    {
        for(int length=1;length<n;length=2*length)
        {
          MergePass(L,length,n);
        }
    }

    算法复杂度

    时间复杂度：先来分析下趟数，
    length=2*length，length<n，那么length=2^m<n,m<log2n
    所以m范围是[0,log2n-1]，共log2n趟。
    然后每次移动元素都是n次，那么时间复杂度是O(nlog2n)。
    空间复杂度：Merge开辟了一个临时动态数组，大小和待排序的序列一样大，鉴于每次调用都释放了内存，因此即使递归次数为log2n，也只要考虑一次调用的内存开销，因此是O(n).