堆排序

基本概念

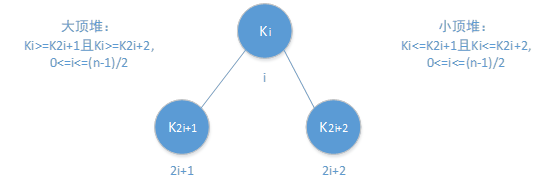
堆，分为大（顶）堆和小（顶）堆，是顺序存储的完全二叉树，并且满足一下特性之一：

(1) 任意非终端结点关键字不小于左右子结点（大堆）

    ki >= k2i+1并且ki>=k2i+2 其中，0 <= i <= (n-1)/2，n是数组元素个数

(2) 任意非终端结点关键字不大于左右子结点（小堆）

    ki <= k2i+1并且ki<=k2i+2 其中，0 <= i <= (n-1)/2，n是数组元素个数


调整
从当前结点（要求是非终端结点）开始，
对于大堆，要求当前结点关键字不小于子结点，如不符合，则将最大的子结点与当前结点交换。循环迭代交换后的子树，确保所有子树都符合大堆特性。

小堆类似

基本思想

堆排序就是利用构建堆和输出堆顶元素的过程，不断对堆进行调整以保证当前结点及其孩子结点满足堆特性，从而达到对初始数组元素进行排序的目的。
核心步骤：

1)构建堆（大堆/小堆）

从最后一个非终端结点开始，向前进行调整，保证当前结点及其子树符合堆特性；

2)输出有序序列

交换堆顶与末尾叶子结点，堆顶输出到数组的有序序列末尾，而不参与堆的调整。从交换后的堆顶开始调整，以确保当前结点及其子树符合堆特性。

实例分析

初始序列 49 38 65 97 76 13 27 49’
位置 0 1 2 3 4 5 6 7

1):构建堆


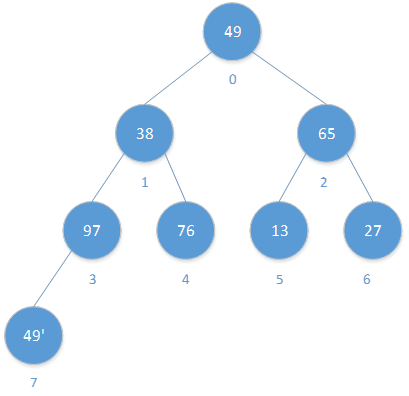
从最后一个非叶子结点开始，向前进行调整，确保符合特性
最后一个非叶子结点位置：(n-1) / 2 = 3, n=8
总共调整次数：(n-1)/2 +1 =4

第1次调整：选择最后一个非叶子结点元素为97（位置3）为当前父结点，与其子结点进行比较，选择最小的结点作为当前父结点。

第一次调整后序列 49 38 65 49’ 76 13 27 97
位置 0 1 2 3 4 5 6 7


第二次调整：选择上一次结点的前一个结点为当前结点进行调整

第二次调整后序列 49 38 13 49’ 76 65 27 97
位置 0 1 2 3 4 5 6 7

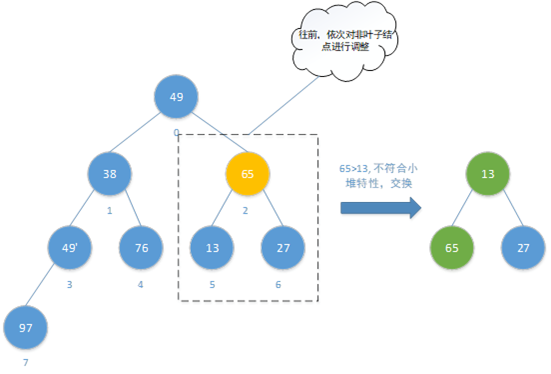
第三次调整：

第三次调整后序列 49 38 13 49’ 76 65 27 97
位置 0 1 2 3 4 5 6 7

第四次调整：

第四次调整后序列 13 38 27 49’ 76 65 49 97
位置 0 1 2 3 4 5 6 7

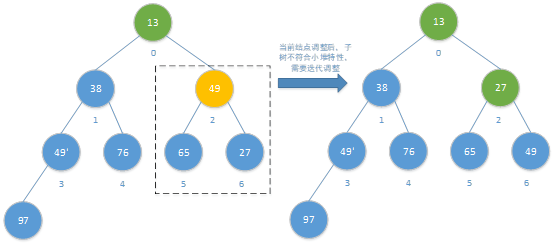
2):输出堆顶元素

将已经构建好的小堆，输出堆顶元素，和末尾元素交换，相当于堆顶移动到数组末尾形成有序序列，未排序元素移动到堆顶。从新的堆顶开始进行调整，直到堆重新符合小堆特性。
交换堆顶和末尾（堆的末尾，不包括已经排好序的部分），并将交换后的堆末尾作为有序序列的一部分，而不再属于堆。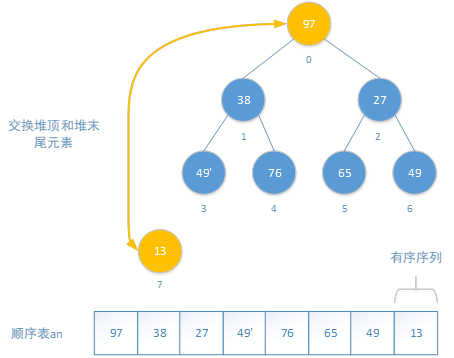

一次交换后，发现97新的位置比子结点大，需要继续调整。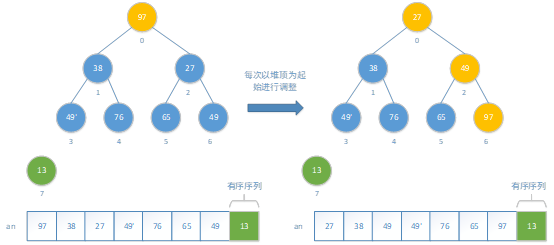

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
void HeapAdjust(List &L,int i,int len)
{
      if(i>len/2-1)   //若无子树，直接退出
        return ;
      for(int k=2*i+1;k<len;k=2*k+1)
      {
        if(k+1<len&&L[k+1]>L[k])
        {
          k++;        //若右孩子比左孩子大，则替换
        }

        if(L[i]<L[k])
        {
          swap(L[i],L[k]);
          i=k;        //以最大子节点为当前结点
        }
        else
          break;      //若满足大堆性质，则直接退出
      }
}

void HeapSort(List &L)
{
    //先建堆
    //从最后一个非叶子结点开始向前调整
    for(int i=L.size/2-1;i>=0;i--)
    {
      HeapAdjust(L,i,L.size);
    }

    //输出并再调整
    for(int j=L.size-1;j>0;j--)
    //j==0没有必要，因为此时只有一个根结点
    {
      swap(L[0],L[j]);
      HeapAdjust(L,0,j);
    }
}

算法复杂度

时间复杂度：
先来考虑建堆的时间，建堆的顺序是用最后一个非叶子结点（从右往左），按bottom-up的方式调用HeapAdjust，
我们可以看一下满二叉树建堆的最坏时间复杂度，

假设最后一层全是叶子结点，高度从叶子结点这层以0开始，则堆的高度为logn-1(没有向下取整，而是精确值)，1/4的调用最多需要1次交换，1/8的调用最多需要2次交换，依次类推，那么时间复杂度的公式就可以表示为：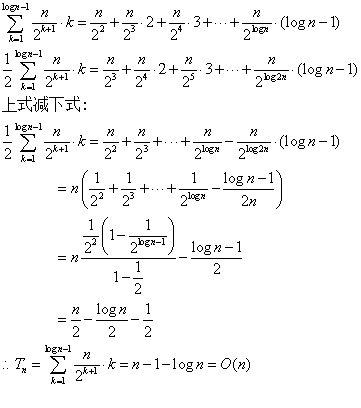

除此，在输出后还需要调整堆，保持堆的性质。
HeapAdjust调整的是根结点，每调整一次，最多需要循环logi-1次，即与堆的高度相等，i是结点个数，HeapAdjust的时间复杂度最好为O(1)而最坏为O(logn),平均为O(logn),共调整n-1次，那么时间复杂度为：

当然，还可用大O算法：O（logn）(n-1)=O(nlogn).

总时间复杂度=O(n)+O(nlogn)=O(nlogn)

空间复杂度：
由于是就地排序，所以是O(1).