计数排序

基本思想

计数排序是一种线性排序算法，它利用了一个数组，因为数组下标的增长是线性的，所以它就把自己的元素转换成新开辟数组的下标。但是数组元素有正有负，下标只有非负值，那么我们就应该考虑如何转换。这也不是很难，只要我们将该元素值减去数组最小值即可得到count数组的下标（类似映射函数）。

例子

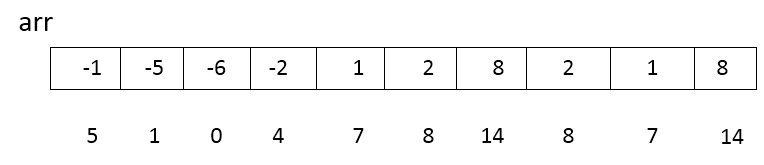
用数组元素减去数组最小值即可得到在count数组的下标。count数组中用橙色框住的表示待排序数组转换后的元素不存在。同时，可以观察到count数组的大小是max-min+1=8+6+1=15.

将count中对应原数组的元素放回数组即可

实现代码

void CountSort(List &L)
{
    int i;
    int min=L[0],max=L[0];
    for(i=1;i<L.size;i++)
    {
      if(L[i]>max)
      {
        max=L[i];
      }
      if(L[i]<min)
      {
        min=L[i];
      }
    }
    int range=max-min+1;
    int *count=new int[range];
    memset(count,0,sizeof(int)*range);

    for(i=0;i<L.size;i++)       //从原数组中取数，原数组个数为size
    {
      count[L[i]-min]++;
    }

    int index=0;
    for(i=0;i<range;i++)        //从开辟的数组中读取，开辟的数组大小为range
    {
      while(count[i]--)
        L[index++]=i+min;
    }
    delete[]count;
}