十大排序——冒泡排序
冒泡排序
基本思想
冒泡排序分为趟数和交换次数。
外层循环为趟数,如果有n个元素则要循环n-1趟。
内层循环主要做每一趟的交换,从第0个元素开始如果发现当前元素大于它的后一个元素,将其交换,每一趟下来,前面的有序区新增一个最小值(相比无序区最小),然后在无序区的第一个元素开始到最后一个元素冒泡排序,将最小值冒出来,以此循环。
最简单的版本
1 | void BubbleSort(List &L) |
严格意义上,这并不能称得上冒泡排序,因为不是比较两个相邻元素,而是直接拿第i个元素和第j个元素对比,这样的话对第i个元素之后的序列没什么帮助。
第一层优化
1 | void BubbleSort_each(List &L) |
相邻两个交换,可以尽量使得除有序区元素外的元素不像上面那么无序
第一趟把2提到了第三位
第二趟把3提到了第四位
数据越多,相邻交换的优势越大。
进一步优化
1 | void BubbleSort_flag(List &L) |
通过设置flag来阻止对已排序序列的循环判断
算术复杂度
最好的情况(全部都是正序的情况下):
比较次数:n-1;
移动次数:0(无数据交换)
最差的情况(全部都是反序的情况下):
比较次数: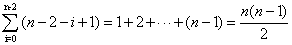
移动次数:同上
综上,时间复杂度:O(n^2)
空间复杂度;O(1)
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Conzxy's blog!
评论






