prim
概述
prim是基于顶点来求得最小生成树,因而适用于稠密图。
基本思想、
维护两个集合VT和ET,ET为所有已确定属于最小生成树的边,VT保存ET的所有边的端点,每一步都将距离VT“最近”但是不属于VT的顶点移入VT。
伪代码
1
2
3
4
5
6
7
| 1 VT←{v},其中v为顶点集V的任意顶点(起始点),ET←∅
2 If VT=V,则输出T={VT,ET},
Else
2.1 在集合E中选取权值最小的边uv,其中u∈VT,v∈V-VT
(如存在多条,选一条即可)
2.2 VT←VT∪{v},ET←ET∪{uv};
2.3 return step 2
|
输入样本
6 10
A B 14
A F 13
A E 22
B F 12
B C 21
C F 18
C D 16
D E 20
D F 19
E F 24
7 11
A B 7
A D 5
B C 8
B D 9
B E 7
C E 5
D E 15
D F 6
E F 8
E G 9
F G 11
0 0
PS:0 0表示终止输入
输出样本
The minimal spanning tree’s vertexes set:
A F B C D E
and its edges:
(A,F) (F,B) (F,C) (C,D) (D,E)
The minimal spanning tree’s vertexes set:
A D F B E C G
and its edges:
(A,D) (D,F) (A,B) (B,E) (E,C) (E,G)
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
| #include <iostream>
#include <vector>
#include <string>
#include <utility>
using namespace std;
int const INF=65536;
string const alphabet("ABCDEFGHIJkLMNOPQRSTUVWXYZ");
char u,v;
int w;
void getMatrix(vector<vector<int>> &g,int numv,int nume)
{
for(int i=0;i<numv;i++)
for(int j=0;j<numv;j++)
{
if(i==j)
g[i].push_back(0);
else
g[i].push_back(INF);
}
for(int i=0;i<nume;i++)
{
cin>>u>>v>>w;
g[u-'A'][v-'A']=g[v-'A'][u-'A']=w;
}
}
void prim(vector<vector<int>> const&g,
vector<int> &VT,vector<pair<int,int>> &ET)
{
int numv=g.size();
VT.push_back(0);
vector<bool> final(numv,false);
final[0]=true;
for(int i=1;i<numv;i++)
{
int min=INF;
int b=0,e=0;
for(auto j=VT.begin();j!=VT.end();j++)
for(int k=0;k<numv;k++)
{
if(!final[k]&&g[*j][k]<min)
{
min=g[*j][k];
b=*j;
e=k;
}
}
final[e]=true;
VT.push_back(e);
ET.push_back(make_pair(b,e));
}
}
void prim1(vector<vector<int>> const&g,
vector<int> &VT,vector<pair<int,int>> &ET)
{
int numv=g.size();
VT.push_back(0);
vector<int> lowcost;
vector<int> adj(numv,0);
for(auto &x:g[0])
lowcost.push_back(x);
for(int i=1;i<numv;i++)
{
int min=INF;
int e=0;
for(int k=0;k<numv;k++)
{
if(lowcost[k]&&lowcost[k]<min)
{
min=lowcost[k];
e=k;
}
}
lowcost[e]=0;
VT.push_back(e);
ET.push_back(make_pair(adj[e],e));
for(int j=0;j<numv;j++)
if(lowcost[j]&&g[e][j]<lowcost[j])
{
lowcost[j]=g[e][j];
adj[j]=e;
}
}
}
int main()
{
int numv,nume;
while(cin>>numv>>nume&&numv>0&&nume>0){
vector<vector<int>> g(numv);
vector<int> VT;
vector<pair<int,int>> ET;
getMatrix(g,numv,nume);
prim(g,VT,ET);
cout<<"The minimal spanning tree's vertexes set:"<<endl;
for(auto &c:VT)
{
cout<<alphabet[c]<<" ";
}
cout<<endl;
cout<<"and its edges:"<<endl;
for(auto &x:ET)
{
cout<<"("<<alphabet[x.first]<<","<<alphabet[x.second]<<")"<<" ";
}
}
}
|
时间复杂度
以下的n表示的就是顶点数v,因为prim是基于顶点的。
第一个版本
最坏情况:
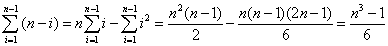
最好情况:
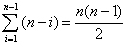
Tn=O(n^3),
主要是寻找最小边权花费了平方时间
第二个版本
这个版本优化了寻找最小边权,只需花费线性时间(空间换时间,但值得),
所以Tn=O(n^2)