Dijkstra

Dijkstra是一种求得从一个顶点出发到达终点最短路径的算法。
Dijkstra本质就是贪心算法，它不是一次求得从起点到终点的最短路径，而是一步步求得它们之间顶点的最短路径，基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

引入概念

点权：

点权值就是源点到该顶点的最短路径（贪心算法必然的结果），下面的D和dist都是存储点权值的vector，将它们输出可以得到源点到各顶点的最短路径。

Dijkstra实现关键——松弛操作

松弛操作是Dijkstra算法的基础操作：如果存在一条从u到v的边，那么从s到v的一条新路径是将边 w(u,v)添加到从s到u的路径尾部来拓展一条从s到v的路径。这条路径的长度是d[u]+w(u,v)。如果这个值比目前已知的d[v]的值要小，那么可以用这个值来替代当前d[v]中的值。松弛边的操作一直运行到所有的d[v]都代表从s到v的最短路径的长度值。松弛操作正是贪心算法的体现。
PS:d[x]表示的是源点到x的最短路径。

基本思想

  • 将起点权值置为0，其他顶点置为无穷大
  • 集合A装所有顶点
  • while A不为空时
    pop出A中最小权值的顶点a
    对a指向的每个顶点x，x的权值设为min（a+arc（a，x），x）

动态演示


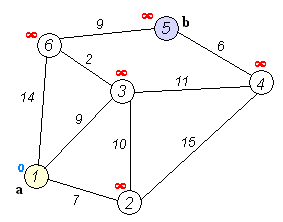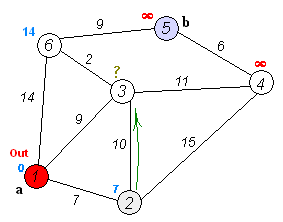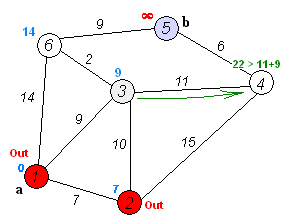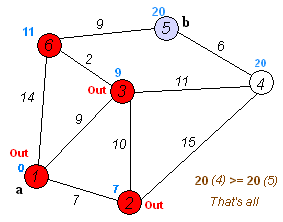
（尽管图上没有显示4和5out，但实际上是要pop的，而且4还要去访问下5，而5的邻接边的顶点都已经访问过了，比较是必然失败的，可设置bool数组记录访问过的顶点来避免重复的比较）

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
//direct是有向依据，numv是顶点个数，nume是边数
void getMatrix(vector<vector<int>> &g,int direct,int numv,int nume)
{
    for(int i=0;i<numv;i++)
        for(int j=0;j<numv;j++)
    {
        if(i==j)
            g[i].push_back(0);
        else
            g[i].push_back(INF);
    }
    for(int i=0;i<nume;i++)
    {   
        int u,v,w;
        cin>>u>>v>>w;
        if(direct==1)
            g[u-1][v-1]=w;
        else
            g[u-1][v-1]=g[v-1][u-1]=w;
    }
}

void Dijkstra(int numv,int v,vector<int>& d,set<int>& p,vector<vector<int>> const&g)
{
    int min,k;  
    vector<bool> final(numv,false);     //记录访问过的顶点
    d[v]=0;                             //v到v的距离为0
    p.insert(v+1);                      //存储源点到终点最短路径的顶点
    final[v]=true;                      //v不需要再访问了=>防止吃回头草
    for(int i=0;i<numv;i++)
    {
      d[i]=g[v][i];                     //记录v的临界边
    }
    for(int i=0;i<numv;i++)
    {
      min=INF;                          //点权设为无穷大
      for(int j=0;j<numv;j++)
      {
        if(!final[j]&&d[j]<min)
        {
          min=d[j];                     //记录当前最小点权
          k=j ;                         //当前最小点权对应顶点
        }
      }
      final[k]=true;                    //记录最小点权的顶点已访问过
      for(int w=0;w<numv;w++)
      {
        //松弛操作体现的就是贪心算法，基于现在的最短路径去求得更远处的最短路径
        if(!final[w]&&min+g[k][w]<d[w]) //若v到k的距离加上k到w的距离比v到w的距离小，则调整v到w的距离
        {
          //松弛操作
          d[w]=min+g[k][w];
          p.insert(k+1);           //p记录w的前驱
        }
      }
    }
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main ()
{
    int numv,nume,direct,u,v,s;
    cin>>numv>>nume>>direct;//顶点数，边数，有向依据

    vector<vector<int>> g(numv);
    getMatrix(g,direct,numv,nume);

    cin>>s;
    vector<int> d(numv);
    set<int> p;
    Dijkstra(numv,s-1,d,p,g);

    return 0;
}

堆优化

运用STL中优先队列的性质可以构造小顶堆（或大顶堆），

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
typedef pair<int,int> ipair;
//adj存入的是顶点邻接边的另一端和边权值
void addedge_non_direct(vector<ipair> *adj,int u,int v,int wt=1)//无向图
{
    //双向记录该边的另一端和边权
    adj[u].push_back(make_pair(v,wt));  
    adj[v].push_back(make_pair(u,wt));
}

void addedge_direct(vector<ipair> *adj,int u,int v,int wt=1)//有向图
{
    //单向记录该边的另一端和边权
    adj[u].push_back(make_pair(v,wt));
}

void Dijkstra_heap(vector<ipair> *adj,int numv,int v)
{
    priority_queue<ipair,vector<ipair>,greater<ipair>> pq;
    //优先队列，按great排序可以构造小根堆，ipair将依次比较first，second
    vector<int> dist(numv,INF);             //将其他点权置为无穷大
    dist[v]=0;                              //源点点权置为0
    vector<bool> final(numv,false);         //防止再度访问
    pq.push(make_pair(0,v));                //将源点放在堆顶
    set<int> p;                             //存储源点到终点最短路径的顶点
    //pq.push(make_pair(dist[v],v));


    while(!pq.empty())
    {
      int u=pq.top().second;                //取当前最小点权值对应的顶点
      pq.pop();

      if(!final[u])                           //已取过的顶点不再遍历
      {
        for(auto x:adj[u])                    //adj[u]的first保存u邻接边的另一端，second保存边权
        {
            int s=x.first;                    //邻接边的另一端
            int weight=x.second;              //邻接边的边权
            if(dist[u]+weight<dist[s]&&!final[s])        //可以松弛
            {
              //松弛操作
              dist[s]=dist[u]+weight;
              pq.push(make_pair(dist[s],s));
              p.insert(u+1);          
            }
        }
        final[u]=true;                      //表示该点的邻接边已经全部访问了并防止吃回头草
      }
  }
    for(int i=0;i<numv;i++)
    {
        if(dist[i]==INF)
        {
          dist[i]=-1;                       //置为-1表示不存在到该顶点的最短路径
        }
        cout<<dist[i]<<" ";                 //输出源点到每个顶点的最短路径
    }
    cout<<endl;
    for(auto &c:p)
      cout<<c<<" ";
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int main ()
{
    int numv,nume,direct,u,v,s;
    cin>>numv>>nume>>direct;//顶点数，边数，有向依据
    vector<ipair> adj[numv];
    for(int i=0;i<nume;i++)
    {
        cin>>u>>v;  //边头部和尾部
        if(direct==0){
            addedge_non_direct(adj,u-1,v-1);  //无权将边权置为1来表示边数，若有权则覆盖默认实参
        }
        else
        {
            addedge_direct(adj,u-1,v-1);
        }
    }
    cin>>s;     //源点
    Dijkstra_heap(adj, numv, s-1);

    return 0;
}

代码部分说明：

!final[u]

我们在取出最小权值点其实要对该点进行判定，因为可能是访问过的顶点，堆中存在两个相同顶点的pair，一个是松弛过的，一个是之前的，当然松弛过的肯定会优先弹出来，这样之前的再弹出来也就没意义了，因此要进行一次判定。

!final[s]

同时，在对最小权值点邻接边进行遍历时，也需要判定是否访问过，因为反向吃回头草必然不能松弛。

实例讲解

无向图没啥好讲的，讲下有向图（无权）吧：

(如果是1开始的，可以在调用函数时令其减一，所以下面都会比图上数字少1)
源点设为1，无权设边权都为1，即边数，dist[0]=0,
1）看1的邻接边只有5，5的点权为∞，因此dist[4]=1，即1到5的最短路径为1；
2）接下来看5的邻接边有6和2，根据一开始压入的顺序决定谁先开始，但是不管谁先都一样，因为小顶堆的性质决定了谁先pop，现在6的点权是∞，所以dist[5]=2；
3）接下来看5的邻接边2，2的点权为∞，所以dist[1]=2；
4）现在pop顶点2，2的邻接边有4，1，但是1不予考虑，俗话说的好：好牛不吃回头草，因为对于访问过的结点，dist[u]+weightdist[2]，更别说加上边权了；
7）pop顶点4，4的邻接边有1，3，但是都是已经访问过的，比较肯定失败；
8）现在优先队列已空，结束while循环，输出源点到各顶点的最小路径后结束函数。

时间复杂度分析

伪代码：

1
2
3
4
5
6
7
8
1  INITIALIZE-SINGLE-SOURCE(G, s)    
2  S ← Ø					//S存储已访问顶点
3  Q ← V[G]            				//Q存储所有顶点
4  while Q ≠ Ø
5      do u ← EXTRACT-MIN(Q)         		//exact_min
6         S ← S ∪{u}
7         for each vertex v ∈ Adj[u]
8             do RELAX(u, v, w)      	        //decrease_key

Tn=O(e·Tdk+v·Tem)，Tdk表示decrease_key的时间复杂度，Tem表示exact_min的时间复杂度，这是因为decrease_key体现在松弛操作，松弛操作需要遍历最小权值点的邻接边,最多遍历所有边，以最多遍历的那次代表其他顶点的松弛，所以是e（Big O），而exact_min与顶点数有关，最坏需要遍历所有顶点（一般版本就是要遍历所有顶点），所以是v。
一般版本的exact_min是通过for循环，最坏遍历所有顶点，所以是O(v),decrease_key很简单，不需要调整最小路径数组，为O(1),那么时间复杂度为O(e+v^2)=O(v^2)，但我们可以通过优先队列来优化，优先队列可以自动进行堆排序，这个维护堆的过程时间复杂度最坏为O(logv),而exact_min的过程堆排序进行为O(logv)，decrease_key的过程需要维护堆也是O(logv)所以堆优化的Dijkstra的时间复杂度为O((e+v)logv),取同阶时间复杂度为O(nlogn)>O(n^2)。